Question

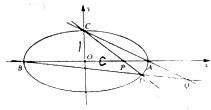过点C（0，1）的椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

3

2

，椭圆与x轴交于两点A（a，0）、B（-a，0），过点C的直线l与椭圆交于另一点D，并与x轴交于点P，直线AC与直线BD交于点Q．
（I）当直线l过椭圆右焦点时，求线段CD的长；
（Ⅱ）当点P异于点B时，求证：

OP

•

OQ

为定值．

Answer 1

分析：（I）当直线l过椭圆右焦点时，写出直线l的方程，并和椭圆联立方程，求得点D的坐标，根据两点间距离公式即可求得线段CD的长；
（Ⅱ）设出直线l的方程，并和椭圆联立方程，求得点D的坐标，并求出点P的坐标，写出直线AC与直线BD的方程，并解此方程组，求得Q点的坐标，代入

OP

•

OQ

即可证明结论．

解答：解：（I）由已知得b=1，

c

a

=

3

2

，解得a=2，
所以椭圆的方程为

x2

4

+  y2=1．
椭圆的右焦点为（

3

，0），此时直线l的方程为y=-

3

3

x+1，
代入椭圆方程化简得7x²-8

3

x=0．
解得x₁=0，x₂=

8 3

7

，代入直线l的方程得y₁=1，y₂=-

1

7

，
所以D点坐标为（

8 3

7

，-

1

7

）
故|CD|=

( 8 3 7 -0)2+(- 1 7 -1)2

=

16

7

；
（Ⅱ）当直线l与x轴垂直时与题意不符，设直线l的方程为y=kx+1（k≠0，k≠

1

2

）
代入椭圆方程化简得（4k²+1）x²+8kx=0，
解得x₁=0，x₂=

-8k

4k2+1

，代入直线l的方程得y₁=1，y₂=

1-4k2

4k2+1

，
所以D点坐标为（

-8k

4k2+1

，

1-4k2

4k2+1

），
又直线AC的方程为

x

2

+y=1，直线BD的方程为y=

1+2k

2-4k

(x+2)，
联立解得

x=-4k y=2k+1

，
因此Q点坐标为（-4k，2k+1），
又P点坐标为（-

1

k

，0），
∴

OP

•

OQ

=（-

1

k

，0）•（-4k，2k+1）=4，
故

OP

•

OQ

为定值．

点评：此题是个难题．本题考查了、直线与椭圆的位置关系及弦长公式，和有关定值定点问题，是一道综合性的试题，考查了学生综合运用知识解决问题的能力．其中问题（II）考查了同学们观察、推理以及创造性地分析问题、解决问题的能力，