题目内容
【题目】若函数![]() 同时满足下列两个条件,则称该函数为“和谐函数”:
同时满足下列两个条件,则称该函数为“和谐函数”:
(1)任意![]() 恒成立;
恒成立;
(2)任意![]() 且
且![]() ,都有
,都有![]()
以下四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中是“和谐函数”的为________________(写出所有正确的题号).
中是“和谐函数”的为________________(写出所有正确的题号).
【答案】③④
【解析】
先由单调性以及奇偶性定义得到 “和谐函数”满足的条件,再以此为依据,分别判断奇偶性以及单调性,即可判断.
任意![]() 恒成立,则任意
恒成立,则任意![]()
即函数![]() 在
在![]() 上为奇函数
上为奇函数
取![]() ,因为任意
,因为任意![]() 且
且![]() ,都有
,都有![]() ,所以
,所以![]()
![]() 在
在![]() 上增函数
上增函数
①函数![]() 的定义域为
的定义域为![]() ,故①不是和谐函数;
,故①不是和谐函数;
②![]() ,令
,令![]()
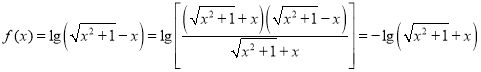 ,则函数
,则函数![]() 在
在![]() 上为奇函数,但
上为奇函数,但![]() ,即不是增函数,故②不是和谐函数;
,即不是增函数,故②不是和谐函数;
③令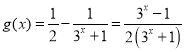 ,定义域为
,定义域为![]()
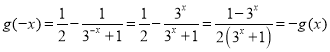 ,则函数
,则函数![]() 在
在![]() 上为奇函数;
上为奇函数;
设![]() ,
,![]()
因为![]() ,所以
,所以![]() ,即
,即![]()
所以函数![]() 在
在![]() 上为增函数,故③为和谐函数;
上为增函数,故③为和谐函数;
④令![]() ,定义域为
,定义域为![]()
![]() ,则函数
,则函数![]() 在
在![]() 上为奇函数;
上为奇函数;
设![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]()
即![]()
即函数![]() 在
在![]() 上为增函数,故④是和谐函数;
上为增函数,故④是和谐函数;
故答案为:③④

练习册系列答案
相关题目