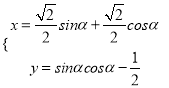Question

【题目】a，b为正数，给出下列命题：

①若a2﹣b2＝1，则a﹣b＜1；

②若＝1，则a﹣b＜1；

③ea﹣eb＝1，则a﹣b＜1；

④若lna﹣lnb＝1，则a﹣b＜1．

其中真命题的有_____．

Answer 1

【答案】①③

【解析】

不正确的结论，列举反例，正确的结论，进行严密的证明，即可得出结论．

①中，a，b中至少有一个大于等于1，则a+b＞1，由a2-b2=（a+b）（a-b）=1，所以a-b＜1，故①正确．

②中＝=1, 只需a-b=ab即可，取a=2，b=,满足上式但a-b=>1故②错；
③构造函数y=x-ex，x＞0，y′=1-ex＜0，函数单调递减，∵ea-eb=1，∴a＞b，∴a-ea＜b-eb，
∴a-b＜ea-eb=1，故③正确；

④若lna-lnb=1，则a=e，b=1，a-b=e-1＞1，故④不正确．

故答案为：①③．