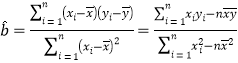题目内容
【题目】如图所示，某镇有一块空地
，其中
，
，
.当地镇政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖
，其中
，
都在边
上，且
，挖出的泥土堆放在
地带上形成假山，剩下的
地带开设儿童游乐场.为安全起见，需在
的周围安装防护网.
（1）当
时，求防护网的总长度；
（2）为节省投入资金，人工湖的面积要尽可能小，问如何设计施工方案，可使的面积最小？最小面积是多少？
【答案】(1) 
；（2）当
时，最小值为
.
【解析】
（1）证明
为正三角形，可得的周长为9，即防护网的总长度为9km；
（2）设
，在
和中使用正弦定理求出
，
，得出
的面积关于
的函数，利用三角函数恒等变换化简，得出面积的最小值.
（1）
在
中，
，
，
，
，
在
中，，
，
，由余弦定理，得
，
，即
，
，
为正三角形，所以的周长为9，即防护网的总长度为.
（2）设 
，
,
,
又在
中，由
，得
，
在
中，由
，得
，
，
当且仅当
，即
时，的面积取最小值为
.
练习册系列答案
相关题目
【题目】某班主任对全班50名学生进行了作业量多少的调查，喜欢玩电脑游戏的同学认为作业多的有18人，认为作业不多的有9人，不喜欢玩电脑游戏的同学认为作业多的有8人，认为作业不多的有15人，则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少？
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
