题目内容
给出下列命题
①在△ABC中,A>B是sinA>sinB的充要条件;
②设m,n是两条直线,α,β是空间中两个平面.若 ,
, ;
;
③函数f(x)= 是周期为2
是周期为2 的偶函数;
的偶函数;
④已知定点A(1,1),抛物线 的焦点为F,点P为抛物线上任意一点,则
的焦点为F,点P为抛物线上任意一点,则 的最小值为2;
的最小值为2;
以上命题正确的是________(请把正确命题的序号都写上)
【答案】
①④
【解析】
试题分析:由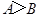 ,三角形的大边对大角可得
,三角形的大边对大角可得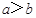 a>b,再由正弦定理可得,
a>b,再由正弦定理可得,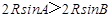 ,即
,即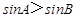 ,反之也成立,故①正确;
,反之也成立,故①正确;
若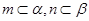 ,
,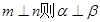 或
或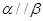 ,故②不正确;
,故②不正确;
因为函数f(x)= 是周期为
是周期为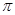 的偶函数,故③错误;
的偶函数,故③错误;
因为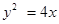 的焦点为
的焦点为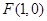 ,准线为
,准线为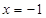 .设点
.设点 在准线上的射影为D,则根据抛物线的定义可知
在准线上的射影为D,则根据抛物线的定义可知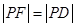 ,
,
∴要使
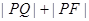 取得最小值,即须
取得最小值,即须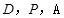 三点共线时
三点共线时 最小为2.故④正确.
最小为2.故④正确.
答案为①④.
考点:充要条件,三角函数的图像和性质,抛物线的定义及其几何性质.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为棱BC,DD1上的点,给出下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为棱BC,DD1上的点,给出下列命题: