题目内容
 如图,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为棱BC,DD1上的点,给出下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为棱BC,DD1上的点,给出下列命题:①在平面ABF内总存在与直线B1E平行的直线;
②若B1E⊥平面ABF,则CE与DF的长度之和为2;
③存在点F使二面角B1-AC-F的大小为45°;
④记A1A与平面ABF所成的角为α,BC与平面ABF所成的角为β,则α+β的大小与点F的位置无关.
其中真命题的序号是
②④
②④
. (写出所有真命题的序号)分析:①在平面CD1内,过点F作FG∥CD,则ABCF四点共面,连接BG,可知直线B1E与平面ABF总相交;
②利用B1E⊥平面ABF,可以证明△B1EB≌△BGC,所以CG=BE,从而可得CE与DF的长度之和为2;
③连接AC,CF,BD,B1A,B1C,AC∩BD=0,则FO⊥AC,B1O⊥AC,从而∠B1OF为二面角B1-AC-F的平面角.由于点F在点D1处时,∠B1OD1>45°,故可得结论;
④确定AD与平面ABF所成的角为β,从而可知∠A1AF=α,∠DAF=β,α+β=90°,故可得结论
②利用B1E⊥平面ABF,可以证明△B1EB≌△BGC,所以CG=BE,从而可得CE与DF的长度之和为2;
③连接AC,CF,BD,B1A,B1C,AC∩BD=0,则FO⊥AC,B1O⊥AC,从而∠B1OF为二面角B1-AC-F的平面角.由于点F在点D1处时,∠B1OD1>45°,故可得结论;
④确定AD与平面ABF所成的角为β,从而可知∠A1AF=α,∠DAF=β,α+β=90°,故可得结论
解答: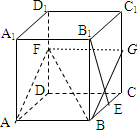 解:①在平面CD1内,过点F作FG∥CD,则ABCF四点共面,连接BG,则BG与B1E一定相交,即直线B1E与平面ABF总相交,故①为假命题;
解:①在平面CD1内,过点F作FG∥CD,则ABCF四点共面,连接BG,则BG与B1E一定相交,即直线B1E与平面ABF总相交,故①为假命题;
②B1E⊥平面ABF,则B1E⊥BG,△B1EB≌△BGC,∴CG=BE,∵CG=DF,BE+CE=2,∴CE与DF的长度之和为2,故②为真命题;
③连接AC,CF,BD,B1A,B1C,AC∩BD=0,则FO⊥AC,B1O⊥AC,∴∠B1OF为二面角B1-AC-F的平面角
当点F在点D1处时,D1O=B1O=
,B1D1=2
,∴cos∠B1OD1=
=
<
,∴∠B1OD1>45°
∴不存在点F使二面角B1-AC-F的大小为45°,故③为假命题;
④∵BC∥AD,BC与平面ABF所成的角为β,∴AD与平面ABF所成的角为β
∵平面ABF⊥平面D1A,∴∠A1AF=α,∠DAF=β,∴α+β=90°,∴α+β的大小与点F的位置无关,故④为真命题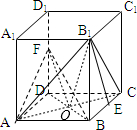
综上知,真命题的序号是②④
故答案为:②④
 解:①在平面CD1内,过点F作FG∥CD,则ABCF四点共面,连接BG,则BG与B1E一定相交,即直线B1E与平面ABF总相交,故①为假命题;
解:①在平面CD1内,过点F作FG∥CD,则ABCF四点共面,连接BG,则BG与B1E一定相交,即直线B1E与平面ABF总相交,故①为假命题;②B1E⊥平面ABF,则B1E⊥BG,△B1EB≌△BGC,∴CG=BE,∵CG=DF,BE+CE=2,∴CE与DF的长度之和为2,故②为真命题;
③连接AC,CF,BD,B1A,B1C,AC∩BD=0,则FO⊥AC,B1O⊥AC,∴∠B1OF为二面角B1-AC-F的平面角
当点F在点D1处时,D1O=B1O=
| 6 |
| 2 |
| 6+6-8 | ||||
2×
|
| 2 |
| 3 |
| ||
| 2 |
∴不存在点F使二面角B1-AC-F的大小为45°,故③为假命题;
④∵BC∥AD,BC与平面ABF所成的角为β,∴AD与平面ABF所成的角为β
∵平面ABF⊥平面D1A,∴∠A1AF=α,∠DAF=β,∴α+β=90°,∴α+β的大小与点F的位置无关,故④为真命题

综上知,真命题的序号是②④
故答案为:②④
点评:本题以正方体为载体,综合考查线面、面面位置关系,考查线面角、面面角,解题时需要一一进行验证,很容易出错.

练习册系列答案
相关题目

 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且