题目内容
给出下列命题:①在△ABC中,若A<B,则sinA<sinB;
②将函数y=sin(2图象向右平移
| π |
| 3 |
③在△ABC中,若AB=2,AC=3,∠ABC=60°,则△ABC必为锐角三角形;
④在同一坐标系中,函数y=sinx的图象和函数y=
| x |
| 2 |
其中真命题是
分析:根据三角形大角对大边及正弦定理的推论,可以判断①的真假;根据正弦函数的平移变换法则,可以判断②的真假;根据正弦定理,我们确定△ABC的三个内角的取值范围,可以判断③的真假;根据正弦型函数的图象和一次函数的图象,我们可以判断④的真假.进而得到答案.
解答:解:由正弦定理得A<B?a<b?2RsinA<2RsinB<sinA<sinB(其中R为△ABC外接圆半径),故①正确;
将函数y=sin(2图象向右平移
个单位,得到函数y=sin(2x-
)的图象,故②错误;
由正弦定理得sin∠ACB=
=
>
,故∠ACB>30°,则∠BAC<90°,故③正确;
在同一坐标系中,函数y=sinx的图象和函数y=
的图象有三个公共点,故④正确;
故答案为:①③④
将函数y=sin(2图象向右平移
| π |
| 3 |
| π |
| 3 |
由正弦定理得sin∠ACB=
| AB•sin∠ABC |
| AC |
| ||
| 3 |
| 1 |
| 2 |
在同一坐标系中,函数y=sinx的图象和函数y=
| x |
| 2 |
故答案为:①③④
点评:本题考查的知识点是命题的真假判断与应用,其中利用三角形的性质,正弦定理,三角函数的图象与性质,正弦函数平移变换法则等基础知识点判断题目中四个命题的真假是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
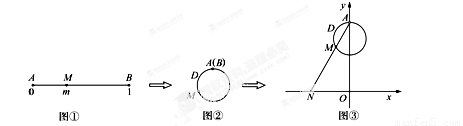
 到实数集R的映射过程:区间
到实数集R的映射过程:区间 围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为 ,则m的象就是n,记作
,则m的象就是n,记作 .
.
 ;
; 在定义域
在定义域 上单调递增;
上单调递增; ;
; 的不等式
的不等式 的解集为
的解集为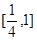 .
.
 ”的否命题为“若
”的否命题为“若 ”
” ”的否定是“
”的否定是“ ”
”