题目内容
15.设函数f(x)=|2x+2|-|x-2|.(Ⅰ)求不等式f(x)>2的解集;
(Ⅱ)若?x∈R,f(x)≥t2-$\frac{7}{2}$t恒成立,求实数t的取值范围.
分析 (Ⅰ)根据函数f(x)=$\left\{\begin{array}{l}{-x-4,x<-1}\\{3x,-1≤x<2}\\{x+4,x≥2}\end{array}\right.$,分类讨论,求得f(x)>2的解集.
(Ⅱ)由f(x)的解析式求得f(x)的最小值为f(-1)=-3,再根据f(-1)≥t2-$\frac{7}{2}$,求得实数t的取值范围.
解答 解:(Ⅰ)函数f(x)=|2x+2|-|x-2|=$\left\{\begin{array}{l}{-x-4,x<-1}\\{3x,-1≤x<2}\\{x+4,x≥2}\end{array}\right.$,
当x<-1时,不等式即-x-4>2,求得x<-6,∴x<-6.
当-1≤x<2时,不等式即3x>2,求得x>$\frac{2}{3}$,∴$\frac{2}{3}$<x<2.
当x≥2时,不等式即x+4>2,求得x>-2,∴x≥2.
综上所述,不等式的解集为{x|x>$\frac{2}{3}$ 或x<-6}.
(Ⅱ)由以上可得f(x)的最小值为f(-1)=-3,若?x∈R,f(x)≥t2-$\frac{7}{2}$t恒成立,
只要-3≥t2-$\frac{7}{2}$t,即2t2-7t+6≤0,求得$\frac{3}{2}$≤t≤2.
点评 题主要考查绝对值不等式的解法,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.在复平面内,复数$\frac{2-3i}{3+2i}$对应的点的坐标为( )
| A. | (0,-1) | B. | $(0,-\frac{13}{9})$ | C. | $(\frac{12}{13},-1)$ | D. | $(\frac{12}{9},-\frac{13}{9})$ |
7.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,若实数a满足$f({log_2}a)+f({log_{\frac{1}{2}}}a)≤2f(1)$,则实数a的取值范围是( )
| A. | (0,2] | B. | $[\frac{1}{2},2]$ | C. | [2,+∞) | D. | $(0,\frac{1}{2}]∪[{2,+∞})$ |
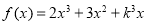 ,在0处的导数为27,则
,在0处的导数为27,则 ( )
( )