题目内容
12．函数f（x）=xe-x在[0，4]上的最小值为（ ）| A． | $\frac{4}{e^4}$ | B． | $\frac{1}{e}$ | C． | 0 | D． | $\frac{2}{e^2}$ |
分析 利用导数求得函数的极值，根据函数的最值定理，求解函数的最小值．
解答 解：函数f（x）=xe-x，
则f′（x）=$\frac{1-x}{{e}^{x}}$，
令f′（x）=0，得x=1，
当x∈[0，1）时，f′（x）＞0，f（x）递增；
当x∈（1，4]时，f′（x）＜0，f（x）递减．
∴x=0时f（x）取得极大值也为最大值，
f（0）=0，f（4）=$\frac{4}{{e}^{4}}$．
函数的最小值为：0．
故选：C．
点评 该题考查利用导数研究函数的最值，属基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
2．命题p：“a＞0且b＞0”，命题q：“方程$\frac{x^2}{a}+\frac{y^2}{b}=1$表示椭圆”，那么p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
7．某农贸市场新上市“绿色蔬菜”，现对其日销售量进行统计，统计结果如下表格．
（1）求m，n的值；
（2）若将表格中的频率看作概率，且每天的销售量互不影响．
①求4天中该“绿色蔬菜”恰好有2天的销售量为2吨的概率；
②已知每吨该“绿色蔬菜”的销售利润为2千元，若ξ表示该“绿色蔬菜”两天销售利润的和（单位：千元），求ξ的分布列和期望．
| 日销售量（吨） | 1 | 2 | 3 |
| 频数 | 10 | 25 | 15 |
| 频率 | 0.2 | m | n |
（2）若将表格中的频率看作概率，且每天的销售量互不影响．
①求4天中该“绿色蔬菜”恰好有2天的销售量为2吨的概率；
②已知每吨该“绿色蔬菜”的销售利润为2千元，若ξ表示该“绿色蔬菜”两天销售利润的和（单位：千元），求ξ的分布列和期望．
17．已知数列{an}满足an+1=2an+1，且首项a1=1，那么a4的值是（ ）
| A． | 7 | B． | 14 | C． | 15 | D． | 8 |
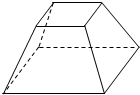（1）画出如图的三视图．