题目内容
在R上定义运算△:x△y=x(1-y)若不等式(x-a)△(x+a)<1,对任意实数x恒成立,则实数a的取值范围是分析:(1)利用定义的运算建立函数关系式,解决恒成立问题转化成图象恒在x轴上方,解△<0即可.
(2)利用配方法求区间内的最值,判定开口和对称轴与区间的位置关系,研究出单调性就可求出值域.
(2)利用配方法求区间内的最值,判定开口和对称轴与区间的位置关系,研究出单调性就可求出值域.
解答:解:(1)根据运算法则得(x-a)△(x+a)=(x-a)(1-x-a)<1
化简得x2-x-a2+a+1>0在R上恒成立,即△<0,解得a∈(-
,
)
(2)y=1-4x-2x2=-2(x+1)2+3在(1,+∞)上是单调减函数
∴当x=1时y=-5,∴y=1-4x-2x2在(1,+∞)的值域是(-∞,-5)
故答案为:(-
,
),(-∞,-5)
化简得x2-x-a2+a+1>0在R上恒成立,即△<0,解得a∈(-
| 1 |
| 2 |
| 3 |
| 2 |
(2)y=1-4x-2x2=-2(x+1)2+3在(1,+∞)上是单调减函数
∴当x=1时y=-5,∴y=1-4x-2x2在(1,+∞)的值域是(-∞,-5)
故答案为:(-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查了函数恒成立问题,以及函数的值域,题目比较新颖,定义了新的运算,属于中档题.

练习册系列答案
相关题目
 :x
:x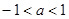 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.