题目内容
【题目】已知f（x）=（2x﹣3）n展开式的二项式系数和为512，且（2x﹣3）n=a0+a1（x﹣1）+a2（x﹣1）2+…+an（x﹣1）n
（1）求a2的值；
（2）求a1+a2+a3+…+an的值．
【答案】
（1）解：（1）由）=（2x﹣3）n展开式的二项式系数和为512，可得2n=512，∴n=9．
∵（2x﹣3）9=[﹣1+2（x﹣1）]9=a0+a1（x﹣1）+a2（x﹣1）2+…+a9（x﹣1）9，
∴a2= 
（﹣1）722=﹣144．
（2）解：在（2x﹣3）9=a0+a1（x﹣1）+a2（x﹣1）2+…+a9（x﹣1）9中，令x=1，可得a0=﹣1．
再令x=2，可得a0+a1+a2+a3+…+an=1，
∴a1+a2+a3+…+an=2．
【解析】（1）利用二项式系数的性质求得n=9，再利用（2x﹣3）9=[﹣1+2（x﹣1）]9以及通项公式求得a2的值．（2）在所给的等式中，令x=1，可得a0=﹣1，再令x=2，可得a0+a1+a2+a3+…+an=1．
【题目】在统计学中，偏差是指个别测定值与测定的平均值之差，在成绩统计中，我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差，班主任为了了解个别学生的偏科情况，对学生数学偏差
（单位：分）与物理偏差
（单位：分）之间的关系进行学科偏差分析，决定从全班56位同学中随机抽取一个容量为8的样本进行分析，得到他们的两科成绩偏差数据如下：
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差 | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差 | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
（1）已知
与
之间具有线性相关关系，求
关于
的线性回归方程；
（2）若这次考试该班数学平均分为118分，物理平均分为90.5，试预测数学成绩126分的同学的物理成绩.
参考公式：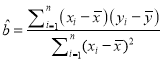 
， 
，
参考数据： 
， 
.