Question

已知抛物线y²=2px（p＞0），椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)，双曲线

x2

a2

-

y2

b2

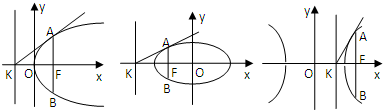
=1(a＞0，b＞0)，如图示，K为与焦点F对应的准线与x轴的交点，AB为过焦点的垂直于x轴的弦．
（1）在抛物线中，已知∠AKB为直角，则在椭圆和双曲线中∠AKB还为直角吗？试证明你的合情推理所得到的结论；
（2）在抛物线中，已知直线KA与抛物线只有一个公共点A，则在椭圆和双曲线中也有类似的性质吗？试选择椭圆证明你的类比推理．

Answer 1

分析：（1）在椭圆与双曲线中，分别求出点K，A的坐标，利用正切定义可得tan∠AKF的大小，进而判断出∠AKB的大小；
（2）在椭圆和双曲线中有相同的性质．由于在椭圆中同（1）可知直线KA的斜率是离心率e，
可得直线KA的方程与椭圆方程联立，可得△=0，即可得出直线KA与椭圆只有一个公共点A．

解答：解：（1）在椭圆中，K(-

a2

c

，0)，A(-c，

b2

a

)，tan∠AKF=

b2 a -0

-c+ a2 c

=

c

a

=e＜1，
∴∠AKF＜45⁰，
得∠AKB=2∠AKF为锐角；                                        
同样，在双曲线中，K(

a2

c

，0)，A(c，

b2

a

)，tan∠AKF=

b2 a -0

c- a2 c

=

c

a

=e＞1，
∴∠AKF＞45⁰，
从而∠AKB=2∠AKF为钝角．                                      
（2）在椭圆和双曲线中有相同的性质．
在椭圆中同（1）可知直线KA的斜率是离心率e，
直线KA的方程为y=

c

a

(x+

a2

c

)，代入b²x²+a²y²=a²b²，得x²+2cx+c²=0，
△=0，x₁=x₂=-c，∴直线KA与椭圆只有一个公共点A．

点评：熟练掌握圆锥曲线的标准方程及其性质、直线与圆锥曲线的位置关系及其判断方法等是解题的关键．