题目内容
3.命题p:不等式ax2-2ax+1>0的解集为R,命题q:不等式$\frac{\sqrt{3}}{4}$sinx+$\frac{1}{4}$cosx-a<0恒成立,若“p∧q”为假命题且“p∨q”为真命题,求实数a的取值范围.分析 分别求出p,q为真时的a的范围,通过讨论p,q的真假,从而求出a的范围.
解答 解:∵函数f(x)=lg(ax2-2ax+1)的定义域为R
∴ax2-2ax+1>0恒成立…(2分)
∴a=0或$\left\{\begin{array}{l}{a>0}\\{△<0}\end{array}\right.$…(4分)
解得0≤a<1…(5分)
又∵不等式$\frac{\sqrt{3}}{4}$sinx+$\frac{1}{4}$cosx-a<0恒成立,
∴a>$\frac{1}{2}$…(8分)
若“p∧q”为假命题且“p∨q”为真命题
则p,q一真一假,
所以0≤a≤$\frac{1}{2}$或a≥1.…(12分)
点评 本题考查了函数恒成立问题,考查复合命题的判断,是一道基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
14.命题p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6相交.则?p及?p的真假为( )
| A. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为真 | |
| B. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为假 | |
| C. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为真 | |
| D. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为假 |
8.已知等差数列{an}中,a7+a9=16,a4=4,则a6的值是( )
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
12.如果幂函数f(x)=xa的图象经过点(4,2),则f(16)的值等于( )
| A. | 16 | B. | 4 | C. | $\frac{1}{16}$ | D. | $\frac{1}{4}$ |
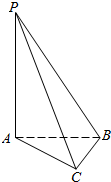 如图,在Rt△ABC中,AC=BC,PA⊥平面ABC,PB与平面ABC成60°角
如图,在Rt△ABC中,AC=BC,PA⊥平面ABC,PB与平面ABC成60°角 若三棱锥的三视图如图,则其表面积为30+6$\sqrt{5}$.
若三棱锥的三视图如图,则其表面积为30+6$\sqrt{5}$.