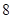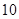题目内容
(本小题满分12分)在数列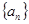 中,
中,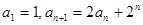 .
.
(1)设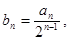 证明
证明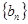 是等差数列;
是等差数列;
(2)求数列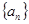 的前
的前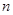 项和
项和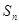 .
.
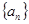 中,
中,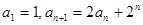 .
.(1)设
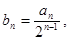 证明
证明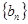 是等差数列;
是等差数列;(2)求数列
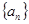 的前
的前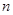 项和
项和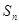 .
.(1)见解析;(2)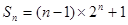
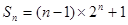
本试题主要是考查了数列的定义的运用,以及通项公式和前n项和的关系适合的运用。
(1)由已知 得,
得,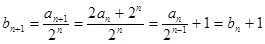 ,然后分析可知
,然后分析可知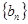 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;
(2)由(1)知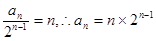 ,然后分析通项公式的特点得到,运用错位相减法得到前n项和的求解的综合运用。
,然后分析通项公式的特点得到,运用错位相减法得到前n项和的求解的综合运用。
解析:(1)由已知 得
得
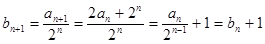 , 又
, 又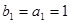
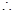
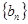 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;
(2)由(1)知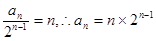
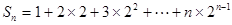 ;
;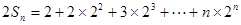
两式相减得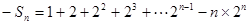
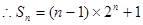
(1)由已知
 得,
得,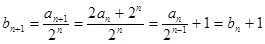 ,然后分析可知
,然后分析可知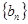 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;(2)由(1)知
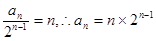 ,然后分析通项公式的特点得到,运用错位相减法得到前n项和的求解的综合运用。
,然后分析通项公式的特点得到,运用错位相减法得到前n项和的求解的综合运用。解析:(1)由已知
 得
得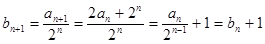 , 又
, 又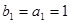
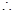
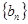 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;(2)由(1)知
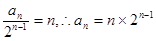
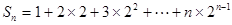 ;
;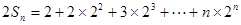
两式相减得
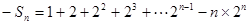
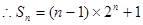

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 的前
的前 项和为
项和为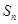 ,点
,点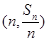 在直线
在直线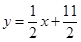 上.数列
上.数列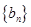 满足
满足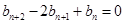
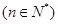 ,
,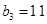 ,且其前9项和为153.
,且其前9项和为153.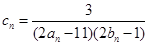 ,数列
,数列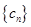 的前
的前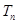 ,求使不等式
,求使不等式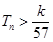 对一切
对一切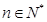 都成立的最大正整数
都成立的最大正整数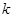 的值.
的值.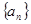 中,
中,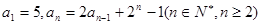 ,若存在实数
,若存在实数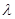 ,使得数列
,使得数列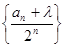 为等差数列,则
为等差数列,则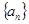 是等差数列,且
是等差数列,且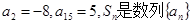 的前n项和,则 ( )
的前n项和,则 ( )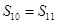 ;
;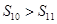 ;
; ;
;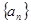 是等差数列,数列
是等差数列,数列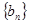 的前n项和
的前n项和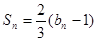 ,若
,若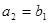 ,
,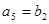 ,(1)求数列
,(1)求数列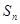 .
.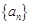 是各项均为正数的等差数列.
是各项均为正数的等差数列.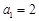 ,且
,且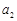 ,
,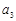 ,
,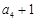 成等比数列,求数列
成等比数列,求数列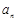 ;
;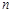 和为
和为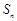 ,设
,设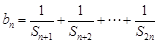 ,若对任意的
,若对任意的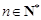 ,不等式
,不等式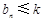 恒成立,求实数
恒成立,求实数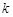 的最小值;
的最小值;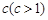 的不同次幂,求证:数列
的不同次幂,求证:数列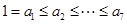 ,其中
,其中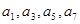 成公比为q的等比数列,
成公比为q的等比数列,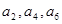 成公差为1的等差数列,则q的最小值是( )
成公差为1的等差数列,则q的最小值是( )



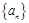 的公差不为零,
的公差不为零,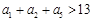 ,且
,且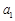 、
、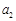 、
、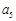 成等比数
成等比数 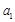 的取值范围为 .
的取值范围为 .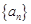 中,若
中,若 ,则
,则 ( )
( )