题目内容
已知椭圆C: 的焦点在y轴上,且离心率为
的焦点在y轴上,且离心率为 .过点M(0,3)的直线l与椭圆C相交于两点A、B.
.过点M(0,3)的直线l与椭圆C相交于两点A、B.
(1)求椭圆C的方程;
(2)设P为椭圆上一点,且满足 (O为坐标原点),当|
(O为坐标原点),当|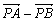 |<
|< 时,求实数λ的取值范围.
时,求实数λ的取值范围.
【答案】
解:(1)由题知a2=m,b2=1,∴ c2=m-1
∴ 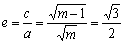 ,解得m=4.
,解得m=4.
∴ 椭圆的方程为 . …………………………………………………4分
. …………………………………………………4分
(2)当l的斜率不存在时,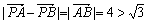 ,不符合条件.
………5分
,不符合条件.
………5分
设l的斜率为k,则l的方程为y=kx+3.
设A(x1,y1),B(x2,y2),P(x0,y0),
联立l和椭圆的方程: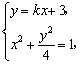 消去y,整理得(4+k2)x2+6kx+5=0,
消去y,整理得(4+k2)x2+6kx+5=0,
∴ Δ=(6k)2-4×(4+k2)×5=16k2-80>0,解得k2>5.
且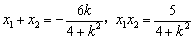 ,
,
∴ 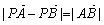
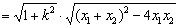 =
=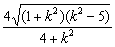 ,
,
由已知有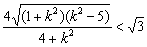 ,
,
整理得13k4-88k2-128<0,解得
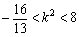 ,
,
∴ 5<k2<8.………………………………………………………………………9分
∵ 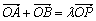 ,即(x1,y2)+(x2,y2)=
λ(x0,y0),
,即(x1,y2)+(x2,y2)=
λ(x0,y0),
∴ x1+x2=λx0,y1+y2=λy0,
当λ=0时,x1+x2=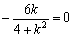 ,
,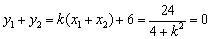 ,
,
显然,上述方程无解.
当λ≠0时,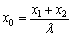 =
=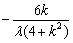 ,
,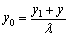
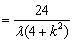 .
.
∵ P(x0,y0)在椭圆上,
∴ 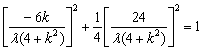 ,
,
化简得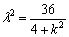 .
.
由 5<k2<8,可得3<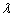 2<4,
2<4,
∴ λ∈(-2,-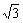 )∪(
)∪(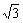 ,2).
,2).
即λ的取值范围为(-2,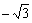 )∪(
)∪(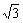 ,2).…………………………………12分
,2).…………………………………12分

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
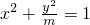 的焦点在y轴上,且离心率为
的焦点在y轴上,且离心率为 .过点M(0,3)的直线l与椭圆C相交于两点A、B.
.过点M(0,3)的直线l与椭圆C相交于两点A、B.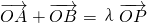 (O为坐标原点),当
(O为坐标原点),当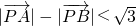 时,求实数λ的取值范围.
时,求实数λ的取值范围.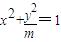 的焦点在y轴上,且离心率为
的焦点在y轴上,且离心率为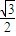 .过点M(0,3)的直线l与椭圆C相交于两点A、B.
.过点M(0,3)的直线l与椭圆C相交于两点A、B.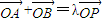 (O为坐标原点),当
(O为坐标原点),当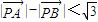 时,求实数λ的取值范围.
时,求实数λ的取值范围.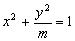 的焦点在y轴上,且离心率为
的焦点在y轴上,且离心率为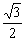 .过点(0,3)的直线l与椭圆C相交于两点A、B.
.过点(0,3)的直线l与椭圆C相交于两点A、B.