Question

（本题满分12分）已知椭圆C：的焦点在y轴上，且离心率为．过点M(0，3)的直线l与椭圆C相交于两点A、B．（1）求椭圆C的方程；（2）设P为椭圆上一点，且满足（O为坐标原点），当||<时，求实数λ的取值范围．

Answer 1

(Ⅰ)   (Ⅱ)  (-2，)∪(，2)

解析:

（1）由题知a²=m，b²=1，∴ c²=m-1∴ ，解得m=4．

∴ 椭圆的方程为．……………4分

（2）当l的斜率不存在时，，不符合条件． ………5分

设l的斜率为k，则l的方程为y=kx+3．设A(x₁，y₁)，B(x₂，y₂)，P(x₀，y₀)，

联立l和椭圆的方程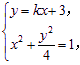：  消去y，整理得(4+k²)x²+6kx+5=0，

∴ Δ=(6k)²-4×(4+k²)×5=16k²-80>0，解得k²>5．且，

∴ =，

由已知有，整理得13k⁴-88k²-128<0，解得 ，

∴ 5<k²<8．………9分∵ ，即(x₁，y₂)+(x₂，y₂)= λ(x₀，y₀)，

∴ x₁+x₂=λx₀，y₁+y₂₌λy₀，当λ=0时，x₁+x₂=，，

显然，上述方程无解．当λ≠0时，=，．

∵ P(x₀，y₀)在椭圆上，∴ ，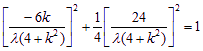

化简得．由 5<k²<8，可得3<²<4，∴ λ∈(-2，-)∪(，2)． 即λ的取值范围为(-2，)∪(，2)．…12分