题目内容
(本题满分14分) 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB= ,AD=3,BB1=1.
,AD=3,BB1=1.
(Ⅰ) 设O是线段BD的中点,
求证:C1O∥平面AB1D1;
(Ⅱ) 求直线AB1与平面ADD1所成的角.

【答案】
(Ⅰ)略
(Ⅰ) 45°.
【解析】
(Ⅰ) 证明:取B1D1的中点E,连结C1E,OA,则A,O,C共线,且 C1E=OA,
因为BCD-B1C1D1为三棱柱,
所以平面BCD∥平面B1C1D1,
故C1E∥OA,
所以C1EAO为平行四边形,
从而C1O∥EA.[来源:Z&xx&k.Com]
又因为C1O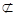 平面AB1D1,
平面AB1D1,
EA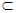 平面AB1D1,
平面AB1D1,
所以C1O∥平面AB1D1.………………………………………………7分
(Ⅱ) 解:过B1在平面B1C1D1内作B1A1∥C1D1,使B1A1=C1D1.
连结A1D1,AA1.
过B1作A1D1的垂线,垂足为F,
则B1F⊥平面ADD1,
所以∠B1AF为AB1与平面ADD1所成的角.
在Rt△A1B1F中,B1F=A1B1 sin 60°=
sin 60°= .
.
在Rt△AB1F中,AB1=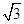 ,
,
故sin∠B1AF =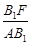 =
=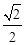 .
.
所以∠B1AF=45°.
即直线AB1与平面ADD1所成角的大小为45°. …………………14分

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目

 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F。
交PB于点F。
 平面
平面 ;
;  平面EFD;
平面EFD;  的大小。
的大小。 .
. 为
为 上的单调函数,试确定实数
上的单调函数,试确定实数 的取值范围;
的取值范围; ,求证:
,求证: .
.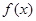 =
=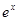 (
(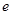 为自然对数的底数),
为自然对数的底数),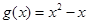 ,记
,记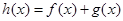 .
.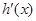 为
为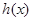 的导函数,判断函数
的导函数,判断函数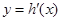 的单调性,并加以证明;
的单调性,并加以证明;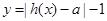 =0有两个零点,求实数
=0有两个零点,求实数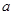 的取值范围.
的取值范围. .
.