题目内容
【题目】已知圆锥曲线 E： 
．
（I）求曲线 E的离心率及标准方程；
（II）设 M（x0 ， y0）是曲线 E上的任意一点，过原点作⊙M：（x﹣x0）2+（y﹣y0）2=8的两条切线，分别交曲线 E于点 P、Q．
①若直线OP，OQ的斜率存在分别为k1 ， k2 ， 求证：k1k2=﹣ 
；
②试问OP2+OQ2是否为定值．若是求出这个定值，若不是请说明理由．
【答案】解：（I）由椭圆定义可知，曲线E是以 
和 
为焦点，长轴长为 
的椭圆，
设椭圆的半长轴长、半短轴长、半焦距分别为a、b、c．
∴ 
， 
，则 
，
∴椭圆的离心率 
，E的标准方程为 
．
（II）①证明：若过原点与⊙M相切的直线斜率存在设为k，
则切线方程为y=kx，∴ 
，
整理得 
．
由题设可知k1 ， k2是以上关于k的一元二次方程的两个实根，
∴ 
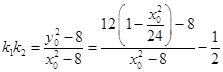，即 
．
②设 P（x1 ， y1），Q（x2 ， y2）．
当直线 O P，OQ的斜率存在时，
由①易得 
， 
，
而 
= 
= 
= 
= 
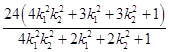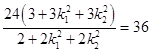
当直线 O P或 OQ的斜率不存在时，圆 M与y轴相切，且圆 M也与x轴相切 P，Q是椭圆 E的两个顶点，∴O P2+OQ2=a2+b2=36．
综上所述：O P2+OQ2为定值36．
【解析】（I）由椭圆定义可知，曲线E是以 
和 
为焦点，长轴长为 
的椭圆，即可得出．（II）①若过原点与⊙M相切的直线斜率存在设为k，则切线方程为y=kx，可得 
，整理得 
．由题设可知k1 ， k2是以上关于k的一元二次方程的两个实根，利用根与系数的关系即可得出．②设 P（x1 ， y1），Q（x2 ， y2）．当直线 O P，OQ的斜率存在时，由①易得 
， 
，利用两点之间的距离、根与系数的关系即可得出．当直线 O P，OQ的斜率不存在时直接验证即可得出．
【题目】为了解学生寒假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表：
本数 | 0 | 1 | 2 | 3 | 4 | 5 |
男生 | 0 | 1 | 4 | 3 | 2 | 2 |
女生 | 0 | 0 | 1 | 3 | 3 | 1 |
（I）从这班学生中任选一名男生，一名女生，求这两名学生阅读名著本数之和为4的概率；
（II）若从阅读名著不少于4本的学生中任选4人，设选到的男学生人数为 X，求随机变量 X的分布列和数学期望；
（III）试判断男学生阅读名著本数的方差 
与女学生阅读名著本数的方差 
的大小（只需写出结论）．
【题目】已知函数f（x）的定义域为[﹣1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示，
x | ﹣1 | 0 | 2 | 4 | 5 |
f（x） | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f（x）的命题：
①函数f（x）的值域为[1，2]；
②如果当x∈[﹣1，t]时，f（x）的最大值为2，那么t的最大值为4；
③函数f（x）在[0，2]上是减函数；
④当1＜a＜2时，函数y=f（x）﹣a最多有4个零点．
其中正确命题的序号是 ． 