��Ŀ����
14����֪����{an}����a1=$\frac{1}{2}$��an+1=an+$\frac{{{a}^{2}}_{n}}{{n}^{2}}$������{bn}����bn=$\frac{{a}_{n}}{n}$����֤����bn�ʣ�0��1��
����֤����$\frac{\frac{1}{{b}_{n+1}}-1}{\frac{1}{{b}_{n}}-1}$=$\frac{{b}_{n}+n+1}{{b}_{n}+n}$
����֤����������������n��an$��\frac{11}{6}$��
���� ��������֪bn=$\frac{{a}_{n}}{n}$��an+1=an+$\frac{{{a}^{2}}_{n}}{{n}^{2}}$���õ�${b}_{n+1}=\frac{{b}_{n}��n+{b}_{n}��}{��n+1��}$��Ȼ��������ѧ���ɷ�֤��0��bn��1��
����${b}_{n+1}=\frac{{b}_{n}��n+{b}_{n}��}{n+1}$���ε�$\frac{1}{{b}_{n+1}}=\frac{n+1}{{b}_{n}��n+{b}_{n}��}$�����$\frac{1}{{b}_{n+1}}-1=\frac{n+1-{b}_{n}��n+{b}_{n}��}{{b}_{n}��n+{b}_{n}��}$����һ�������ô𰸣�
�����ɣ��Ľ��۵õ�$\frac{1}{{b}_{n}}-1=��\frac{1}{{b}_{1}}-1��•\frac{{b}_{1}+2}{{b}_{1}+1}•\frac{{b}_{2}+3}{{b}_{2}+2}��\frac{{b}_{n-1}+n}{{b}_{n-1}+n-1}$��������õ�${b}_{n}��\frac{2}{n+3}$��Ȼ����${a}_{n+1}={a}_{n}+{{b}_{n}}^{2}$֪����n��2ʱ��
${a}_{n}={a}_{1}+{{b}_{1}}^{2}+{{b}_{2}}^{2}+��+{{b}_{n-1}}^{2}$$��{a}_{1}+4��\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}+��+\frac{1}{��n+2��^{2}}��$���ٷŴ�֤�ô𰸣�
��� ֤����������bn=$\frac{{a}_{n}}{n}$����an+1=an+$\frac{{{a}^{2}}_{n}}{{n}^{2}}$����$��n+1��{b}_{n+1}=n{b}_{n}+{{b}_{n}}^{2}$��
��${b}_{n+1}=\frac{{b}_{n}��n+{b}_{n}��}{��n+1��}$����������ѧ���ɷ�֤����0��bn��1��
����a1=$\frac{1}{2}$�ʣ�0��1����֪0��b1��1��
�ڼ���0��bk��1����${b}_{k+1}=\frac{{b}_{k}��k+{b}_{k}��}{��k+1��}$��
��0��bk��1����$0��\frac{k+{b}_{k}}{k+1}��1$����0��bk+1��1��
���ϣ���n��N*ʱ��bn�ʣ�0��1����
������${b}_{n+1}=\frac{{b}_{n}��n+{b}_{n}��}{n+1}$���ɵã�$\frac{1}{{b}_{n+1}}=\frac{n+1}{{b}_{n}��n+{b}_{n}��}$��
��$\frac{1}{{b}_{n+1}}-1=\frac{n+1-{b}_{n}��n+{b}_{n}��}{{b}_{n}��n+{b}_{n}��}$=$\frac{��1-{b}_{n}����1+{b}_{n}+n��}{{b}_{n}��n+{b}_{n}��}$=$��\frac{1}{{b}_{n}}-1��•\frac{{b}_{n}+n+1}{{b}_{n}+n}$��
��$\frac{\frac{1}{{b}_{n+1}}-1}{\frac{1}{{b}_{n}}-1}=\frac{{b}_{n}+n+1}{{b}_{n}+n}$��
�����ɣ��ã�$\frac{1}{{b}_{n}}-1=��\frac{1}{{b}_{1}}-1��•\frac{{b}_{1}+2}{{b}_{1}+1}•\frac{{b}_{2}+3}{{b}_{2}+2}��\frac{{b}_{n-1}+n}{{b}_{n-1}+n-1}$
$�ݣ�\frac{1}{{b}_{1}}-1��•\frac{3}{2}•\frac{4}{3}��\frac{n+1}{n}$��
��${b}_{n}��\frac{2}{n+3}$��
��${a}_{n+1}={a}_{n}+{{b}_{n}}^{2}$֪����n��2ʱ��
${a}_{n}={a}_{1}+{{b}_{1}}^{2}+{{b}_{2}}^{2}+��+{{b}_{n-1}}^{2}$$��{a}_{1}+4��\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}+��+\frac{1}{��n+2��^{2}}��$
$��{a}_{1}+4��\frac{1}{3��4}+\frac{1}{4��5}+��+\frac{1}{��n+1����n+2��}��$=$\frac{1}{2}+4��\frac{1}{3}-\frac{1}{n+2}����\frac{11}{6}$��
���� ���⿼�������е���ʽ������������ѧ���ɷ�֤������Ȼ���йص����⣬ѵ���˷�����֤�����в���ʽ���Ե���ʽ��ѭ��������֤������Ĺؼ���������ѧ������˼ά�����������������������ѹ���⣮

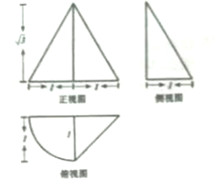
| A�� | $\frac{����+2��\sqrt{3}}{12}$ | B�� | $\frac{����+1��\sqrt{3}}{12}$ | C�� | $\frac{��2��+1��\sqrt{3}}{12}$ | D�� | $\frac{��2��+3��\sqrt{3}}{12}$ |
 ���ڽ�
���ڽ�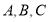 ���Եı߷ֱ�Ϊ
���Եı߷ֱ�Ϊ ����
����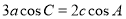 ��
��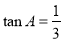 �����
����� �Ķ���Ϊ�� ��
�Ķ���Ϊ�� �� B��
B�� C��
C�� D��
D��