题目内容
3.满足“a∈A且8-a∈A,8-a∈N,a∈N”的有且只有2个元素的集合A的个数是4.分析 根据条件a∈A且8-a∈A,a∈N且8-a∈N,确定元素与元素之间的关系,即可得到满足条件的集合A;
解答 解:∵a∈A且8-a∈A,a∈N且8-a∈N,
若a=0,则8-a=8,此时A={0,8}满足要求;
若a=1,则8-a=7,此时A={1,7}满足要求;
若a=2,则8-a=6,此时A={2,6}满足要求;
若a=3,则8-a=5,此时A={3,5}满足要求;
若a=4,则8-a=4,此时A={4}不满足要求;
故有且只有2个元素的集合A有4个,
故答案为:4.
点评 本题主要考查元素和集合关系的判断和推理.根据条件确定集合元素之间的关系是解决本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.已知函数y=f(x)的图象如图,那么f(x)的表达式为( )
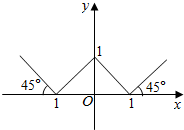

| A. | $\sqrt{{x}^{2}-2x+1}$ | B. | $\sqrt{{x}^{2}-2|x|+1}$ | C. | |x2-1| | D. | -2|x|+1 |
11.若函数f(x)的定义域为[0,1],值域为[1,2],则函数f(x+2)的定义域,值域分别为( )
| A. | [0,1],[1,2] | B. | [2,3],[3,4] | C. | [-2,-1],[1,2] | D. | [-2,-1],[3,4] |