题目内容
设a=
dx,tanβ=3,则tan(α+β)= .
| ∫ | 1 0 |
| 1-x2 |
考点:定积分,两角和与差的正切函数
专题:导数的概念及应用,三角函数的图像与性质
分析:本题可以先利用曲线y=
,x∈[0,1]与x轴围成的图形面积求出a=
dx,再用两角与差的正切公式求出tan(α+β)的值,得到本题结论.
| 1-x2 |
| ∫ | 1 0 |
| 1-x2 |
解答:
解:设y=
,
则有:x2+y2=1,圆的半径r=1,(y≥0),
当x∈[0,1]时,曲线y=
与x轴围成的图形面积为:
S=
×πr2=
.
∵α=
dx,
∴α=
.
∴tanα=1.
∵tanβ=3,
∴tan(α+β)=
=
=-2.
故答案为:-2.
| 1-x2 |
则有:x2+y2=1,圆的半径r=1,(y≥0),
当x∈[0,1]时,曲线y=
| 1-x2 |
S=
| 1 |
| 4 |
| π |
| 4 |
∵α=
| ∫ | 1 0 |
| 1-x2 |
∴α=
| π |
| 4 |
∴tanα=1.
∵tanβ=3,
∴tan(α+β)=
| tanα+tanβ |
| 1-tanα•tanβ |
| 1+3 |
| 1-1×3 |
故答案为:-2.
点评:本题考查了定积分的几何意义、两角和与差的正切公式,本题难度不大,属于基础题.

练习册系列答案
相关题目
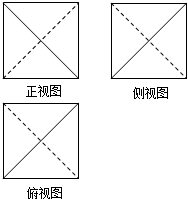 某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )A、
| ||||
| B、3π | ||||
| C、π | ||||
D、
|
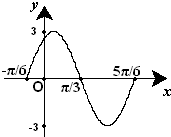 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.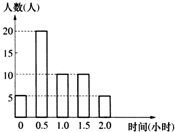 某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为
某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为