题目内容
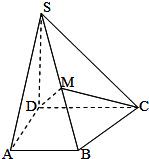 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=| 2 |
(Ⅰ)求证:平面SAB⊥平面SAD;
(Ⅱ)设SB的中点为M,当
| CD |
| AB |
分析:(Ⅰ)先由∠A=90°?AB⊥AD再利用SD⊥平面ABCD?SD⊥AB?AB⊥平面SAD?结论成立.
(Ⅱ)由题中条件可推得DM⊥SB.当
=2时,又可利用其推得BC⊥平面SBD?DM⊥BC?DM⊥平面SBC?DM⊥MC.
(Ⅱ)由题中条件可推得DM⊥SB.当
| CD |
| AB |
解答: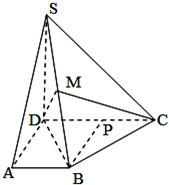 解:(Ⅰ)证明:∵∠A=90°,
解:(Ⅰ)证明:∵∠A=90°,
∴AB⊥AD.
又SD⊥平面ABCD,AB?平面ABCD,
∴SD⊥AB.(2分)
∴AB⊥平面SAD.(4分)
又AB?平面SAB,
∴平面SAB⊥平面SAD(7分)
(Ⅱ)当
=2时,能使DM⊥MC.(9分)
连接BD,∵∠A=90°,AB=AD=a
∴BD=
a∴SD=BD,∠BDA=45°
又M为SB中点,
∴DM⊥SB①(8分)
设CD的中点为P,连接BP,则DP∥AB,且DP=AB
∴BP∥AD,
∴BP⊥CD∴BD=BC
又∠BDC=90°-∠BDA=45°
∴∠CBD=90°即BC⊥BD
又BC⊥SD∴BC⊥平面SBD
∴DM⊥BC②(12分)
由①②知DM⊥平面SBC
∴DM⊥MC
即当
=2时,能使DM⊥MC.(14分)
 解:(Ⅰ)证明:∵∠A=90°,
解:(Ⅰ)证明:∵∠A=90°,∴AB⊥AD.
又SD⊥平面ABCD,AB?平面ABCD,
∴SD⊥AB.(2分)
∴AB⊥平面SAD.(4分)
又AB?平面SAB,
∴平面SAB⊥平面SAD(7分)
(Ⅱ)当
| CD |
| AB |
连接BD,∵∠A=90°,AB=AD=a
∴BD=
| 2 |
又M为SB中点,
∴DM⊥SB①(8分)
设CD的中点为P,连接BP,则DP∥AB,且DP=AB
∴BP∥AD,
∴BP⊥CD∴BD=BC
又∠BDC=90°-∠BDA=45°
∴∠CBD=90°即BC⊥BD
又BC⊥SD∴BC⊥平面SBD
∴DM⊥BC②(12分)
由①②知DM⊥平面SBC
∴DM⊥MC
即当
| CD |
| AB |
点评:本题考查平面和平面垂直的判定和性质.在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则