题目内容
(2012•汕头一模)半径为R的圆周上任取A、B、C三点,则三角形ABC为锐角三角形的概率为( )
分析:法一:三个点在圆上构成三角形,不外乎就三种:钝角三角形,直角三角形和锐角三角形.成钝角三角形和成锐角三角形的概率相同,构成两种三角形的概率和等于成直角三角形的概率.
法二:按逆时针方向依次重新标记三点为A,B,C,设弧AB=x,弧BC=y,弧CA=2π-x-y,根据题意建立关于x,y的约束条件,利用线性质规划的方法求解.
法二:按逆时针方向依次重新标记三点为A,B,C,设弧AB=x,弧BC=y,弧CA=2π-x-y,根据题意建立关于x,y的约束条件,利用线性质规划的方法求解.
解答:解:法一:任意三个点,连接其中两点,
(1)如果两点的连线在直径上,则与第三点构成的三角形是直角三角形,因为直径平分圆,所以概率为
;
(2)如果两点的连线不在直径上,则与第三点构成的三角形,要么是锐角三角形,要么是钝角三角形,所以成钝角三角形和成锐角三角形的概率相同,各是
,
法二:如图①,按逆时针方向依次重新标记三点为A,B,C,设弧AB=x,弧BC=y,弧CA=2π-x-y,
显然:
,三点组成锐角三角形,则
,
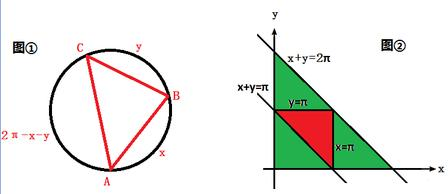
作出图形,如图所示.
所求概率等于图②中红色部分(直线x=π,y=π,x+y=π围成三角形)面积除以所有涂色(红色和绿色)部分(x轴,y轴与直线x+y=2π围成三角形)面积,
为
=
.
故选A.
(1)如果两点的连线在直径上,则与第三点构成的三角形是直角三角形,因为直径平分圆,所以概率为
| 1 |
| 2 |
(2)如果两点的连线不在直径上,则与第三点构成的三角形,要么是锐角三角形,要么是钝角三角形,所以成钝角三角形和成锐角三角形的概率相同,各是
| 1 |
| 4 |
法二:如图①,按逆时针方向依次重新标记三点为A,B,C,设弧AB=x,弧BC=y,弧CA=2π-x-y,
显然:
|
|

作出图形,如图所示.
所求概率等于图②中红色部分(直线x=π,y=π,x+y=π围成三角形)面积除以所有涂色(红色和绿色)部分(x轴,y轴与直线x+y=2π围成三角形)面积,
为
π×π×
| ||
2π×2π×
|
| 1 |
| 4 |
故选A.
点评:本题考查几何概型的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
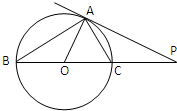 (2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为
(2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为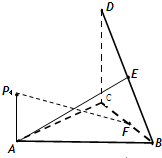 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.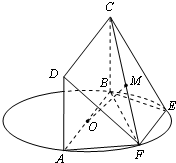 (2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.