Question

5．如图，直角梯形CDEM中，CD∥EM，ED⊥CD，B是EM上一点，且CD=BM=$\sqrt{2}$CM=2，EB=ED=1，沿BC把△MBC折起得到△ABC，使平面ABC⊥平面BCDE．
（Ⅰ）证明：平面EAD⊥平面ACD．
（Ⅱ）求二面角E-AD-B的大小．

Answer 1

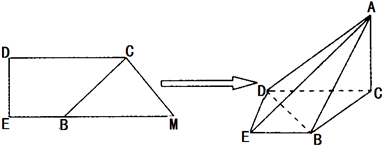
分析 （Ⅰ）过B作BH⊥CD于H，通过勾股定理可得AC⊥BC，利用面面垂直的性质定理及判定定理可得结论；
（Ⅱ）以D为原点，建立如图所示的空间直角坐标系D-xyz，则所求角的余弦值为平面ADE的一个法向量与平面ABD的一个法向量的夹角的余弦值的绝对值，计算即可．

解答 （Ⅰ）证明：过B作BH⊥CD于H，则CH=BH=1，∴BC=$\sqrt{2}$，
又AC=$\sqrt{2}$，AB=2，∴AC²+BC²=AB²，∴AC⊥BC，
又∵平面ABC⊥平面BCDE，且平面ABC∩平面BCDE=BC，
∴AC⊥平面BCDE，∴AC⊥DE，
又CD⊥DE，AC∩CD=C，∴DE⊥平面ACD，
又DE?平面EAD，∴平面EAD⊥平面ACD；
（Ⅱ）解：以D为原点，建立如图所示的空间直角坐标系D-xyz，
由题意可知D（0，0，0），E（1，0，0），A（0，2，$\sqrt{2}$），B（1，1，0），
则$\overrightarrow{DA}$=（0，2，$\sqrt{2}$），$\overrightarrow{DE}$=（1，0，0），$\overrightarrow{DB}$=（1，1，0），
设平面ADE的一个法向量为$\overrightarrow{m}$=（x₁，y₁，z₁），
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DA}=0}\\{\overrightarrow{m}•\overrightarrow{DE}=0}\end{array}\right.$，得$\left\{\begin{array}{l}{2{y}_{1}+\sqrt{2}{z}_{1}=0}\\{{x}_{1}=0}\end{array}\right.$，可取$\overrightarrow{m}$=（0，-1，$\sqrt{2}$），
设平面ABD的一个法向量为$\overrightarrow{n}$=（x₂，y₂，z₂），
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DA}=0}\\{\overrightarrow{n}•\overrightarrow{DB}=0}\end{array}\right.$，得$\left\{\begin{array}{l}{2{y}_{2}+\sqrt{2}{z}_{2}=0}\\{{x}_{2}+{y}_{2}=0}\end{array}\right.$，可取$\overrightarrow{n}$=（1，-1，$\sqrt{2}$），
于是$cos＜\overrightarrow{m}，\overrightarrow{n}＞$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{3}{\sqrt{3}×2}$=$\frac{\sqrt{3}}{2}$，
由题意可知，所求二面角是锐二面角，
∴所求二面角E-AD-B的大小是$\frac{π}{6}$．

点评 本题考查直线与平面垂直的判定，二面角的计算，面面垂直的判定，考查空间想象能力，计算能力，注意解题方法的积累，属于中档题．