题目内容
【题目】已知函数![]() ,
,![]() ,且
,且![]() 与
与![]() 的图象有一个斜率为1的公切线(
的图象有一个斜率为1的公切线(![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() ;
;
(2)设函数![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)由![]() 与
与![]() 的图象有一个斜率为1的公切线,分别对
的图象有一个斜率为1的公切线,分别对![]() 与
与![]() 求导并求出切线方程,列出等量关系可得
求导并求出切线方程,列出等量关系可得![]() ;
;
(2)利用换元将![]() 转化为二次函数,分类讨论对其单调性,对图像特点进行分析,分情况讨论出函数
转化为二次函数,分类讨论对其单调性,对图像特点进行分析,分情况讨论出函数![]() 的零点个数.
的零点个数.
(1)![]() 可得
可得![]() .
.
![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
![]()
![]() .
.
![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
![]() ,
,
故![]()
可得![]() .
.
(2)由(1)可得![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() 时,
时,![]() 有两根,
有两根,
![]() 且
且![]() ,
,
![]() ,
,
得:![]() ,
,
在![]() 上,
上,![]() ,
,
在![]() 上,
上,![]() ,
,
此时,![]() .
.
又![]() 时,
时,![]() 时,
时,![]() .
.
故在![]() 和
和![]() 上,
上,
![]() 各有1个零点.
各有1个零点.
![]() 时,
时,![]()
![]() 最小值为
最小值为![]() ,故
,故![]() 仅有1个零点.
仅有1个零点.
![]() 时,
时,![]() .
.
其中![]() ,同
,同![]() ,
,
![]() 在
在![]() 与
与![]() 上,
上,
![]() 各有1个零点,
各有1个零点,
![]() 时,
时,![]() ,仅在
,仅在![]() 有1个零点,
有1个零点,
![]() 时,对方程
时,对方程![]() .
.
方程有两个正根![]() ,
,![]() .
.
在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,在
,在![]() ,
,![]() .
.
由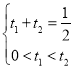 ,可得
,可得![]() ,
,
故![]() .
.
![]()
![]()
![]() ,
,
故![]() .
.
故在![]() 上,
上,![]() ,
,
在![]() 上,
上,![]() ,
,
在![]() 上,
上,![]() 有1个零点:
有1个零点:![]() .
.
![]() 时,
时,![]() 恒成立,
恒成立,
![]() 为增函数,
为增函数,![]() 仅有1个零点:
仅有1个零点:![]() .
.
综上,![]() 或
或![]() 时,
时,![]() 有1个零点,
有1个零点,
![]() 或
或![]() 时,
时,![]() 有2个零点.
有2个零点.

【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
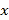
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式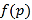 .
.


