题目内容
对于数列{an},如果存在正实数M,使得数列中每一项的绝对值均不大于M,那么称该数列为有界的,否则称它为无界的.在以下各数列中,无界的数列为( )
| A.a1=2,an+1=-2an+3 | B.a1=2,an+1=
| ||
| C.a1=2,an+1=arctanan+1 | D.a1=2,an+1=2
|
∵a1=2,an+1=-2an+3
∴an+1-1=-2(an-1)即{an-1}是首项为1,公比为-2的等比数列
∴an-1=(-2)n-1即an=(-2)n-1+1
|an|=|(-2)n-1+1|当n取无穷大时,|an|也趋向无穷大
∴该数列为无界的.
故选A.
∴an+1-1=-2(an-1)即{an-1}是首项为1,公比为-2的等比数列
∴an-1=(-2)n-1即an=(-2)n-1+1
|an|=|(-2)n-1+1|当n取无穷大时,|an|也趋向无穷大
∴该数列为无界的.
故选A.

练习册系列答案
相关题目
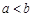 ,则
,则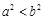 ;
;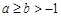 ,则
,则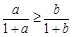 ;
;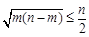 ;
; 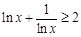 .
.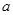 、
、 、
、 ,
, ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )


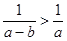
 ,当非零实数a,b满足
,当非零实数a,b满足 ,且使
,且使 最大时,
最大时, 的最小值为 .
的最小值为 . ,的通项公式的是 。
,的通项公式的是 。