题目内容
1.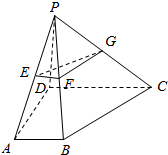 如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.
如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.(1)若点M∈平面EFG,且与点E不重合,判断直线EM与平面ABCD的关系,并说明理由;
(2)若PB=4,求四棱锥C-ABFE的体积.
分析 (1)利用三角形中位线的性质结合面面平行的判定定理得到面EFG∥面ABCD,然后可得直线EM∥平面ABCD;
(2)C到平面ABEF的距离为AD=3,梯形ABEF中,EF=$\frac{1}{2}$,AB=1,高BF=2,面积为$\frac{1}{2}•(\frac{1}{2}+1)×2$=$\frac{3}{2}$,直接代入棱锥的体积得答案.
解答  解:(1)如图,直线EM∥平面ABCD.
解:(1)如图,直线EM∥平面ABCD.
事实上:
∵E,F,G分别为PA,PB,PC的中点,
∴EF∥AB,FG∥BC,EF∩FG=F,AB∩BC=B,
∴平面EFG∥平面ABC,
∵点M∈平面EFG,且与点E不重合,∴直线EM∥平面ABCD;
(2)∵直线PB⊥平面EFG,∴C到平面ABEF的距离为AD=3
梯形ABEF中,EF=$\frac{1}{2}$,AB=1,高BF=2,面积为$\frac{1}{2}•(\frac{1}{2}+1)×2$=$\frac{3}{2}$,
∴四棱锥C-ABFE的体积V=$\frac{1}{3}•\frac{3}{2}•3$=$\frac{3}{2}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率e∈[$\sqrt{2}$,2],则其渐近线的倾斜角的取值范围是( )
| A. | [$\frac{π}{4}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{3π}{4}$] | B. | [$\frac{π}{6}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{5π}{6}$] | C. | [$\frac{π}{6}$,$\frac{π}{4}$]∪[$\frac{4π}{3}$,$\frac{5π}{6}$] | D. | [$\frac{π}{4}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{5π}{5}$] |
6.已知两定点A(-2,1),B(1,3),动点P在直线x-y+1=0上,当|PA|+|PB|取最小值时,这个最小值为( )
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |
11.偶函数f(x)的定义域为R,若f(x+2)为奇函数,且f(1)=1,则f(89)+f(90)为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |

 如图,这是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.
如图,这是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点. 如图,在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,则正三棱锥A-BCD的体积是$\frac{\sqrt{2}}{3}$.
如图,在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,则正三棱锥A-BCD的体积是$\frac{\sqrt{2}}{3}$.