题目内容
若点P是曲线y=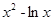 上任意一点,则点P到直线y=x-2的最小距离是 ( )
上任意一点,则点P到直线y=x-2的最小距离是 ( )
A.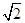 | B.1 | C.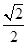 | D.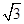 |
A
解析试题分析:点P是曲线y=x2-lnx上任意一点,
当过点P的切线和直线y=x-2平行时,
点P到直线y=x-2的距离最小.
直线y=x-2的斜率等于1,
令y=x2-lnx的导数 y′=2x-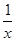 =1,x=1,或 x=-
=1,x=1,或 x=-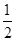 (舍去),
(舍去),
故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于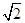 ,
,
故点P到直线y=x-2的最小距离为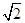 ,
,
故选A.
考点:本题主要考查点到直线的距离公式的应用,函数的导数的求法及导数的几何意义。
点评:运用导数的几何意义曲线,将y=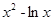 上任意一点P到直线y=x-2的最小距离计算,转化成为求两平行直线之间距离,体现了转化与化归的数学思想.
上任意一点P到直线y=x-2的最小距离计算,转化成为求两平行直线之间距离,体现了转化与化归的数学思想.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
曲线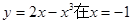 处的切线方程为( )
处的切线方程为( )
A.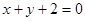 | B. |
C.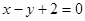 | D.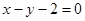 |
设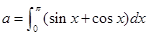 ,则二项
,则二项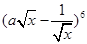 式展开式中x2项的系数是
式展开式中x2项的系数是
| A.-192 | B.193 | C.-6 | D.7 |
若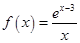 ,则
,则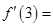 ( )
( )
A.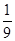 | B.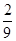 | C.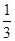 | D.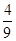 |
已知函数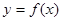 的大致图象如图所示, 则函数
的大致图象如图所示, 则函数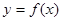 的解析式应为( )
的解析式应为( )
A. | B.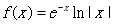 |
C. | D.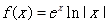 |
某物体的位移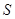 (米)与时间
(米)与时间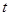 (秒)的关系是
(秒)的关系是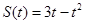 ,则物体在
,则物体在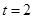 秒时的瞬时速度为( )
秒时的瞬时速度为( )
A.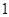 m/s m/s | B.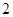 m/s m/s | C. m/s m/s | D.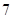 m/s m/s |
已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为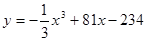 ,则使该生产厂家获得最大年利润的年产量为( )
,则使该生产厂家获得最大年利润的年产量为( )
| A. 13万件 | B. 11万件 | C. 9万件 | D. 7万件 |
 是函数
是函数 的导函数,
的导函数,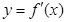 的图象如图所示,则
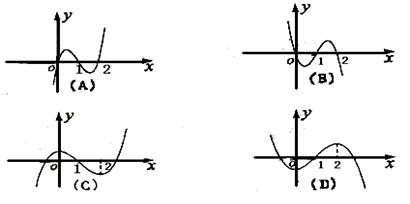
的图象如图所示,则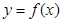 的图象最有可能的是( )
的图象最有可能的是( )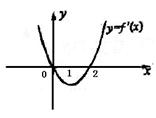
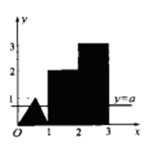
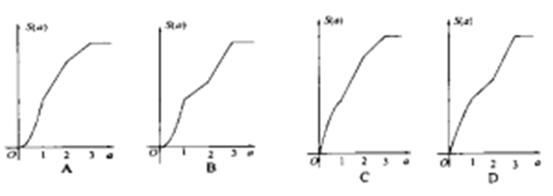
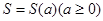 是图1中阴影部分介于平等线
是图1中阴影部分介于平等线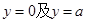 之间的那一部分的面积,则函数
之间的那一部分的面积,则函数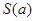 的图象大致为( )
的图象大致为( )