题目内容
13.在四边形ABCD中,设$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{c}$,则$\overrightarrow{CD}$等于( )| A. | $\overrightarrow{c}$-($\overrightarrow{a}$+$\overrightarrow{b}$) | B. | $\overrightarrow{b}$-($\overrightarrow{a}+\overrightarrow{c}$) | C. | $\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | D. | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ |
分析 作出四边形ABCD,结合向量加法法则利用数形结合思想求解.
解答 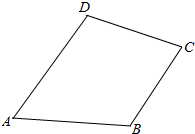 解:∵在四边形ABCD中,设$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{c}$,
解:∵在四边形ABCD中,设$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{c}$,
∴$\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b})$=$\overrightarrow{AD}+\overrightarrow{BA}+\overrightarrow{CB}$=$\overrightarrow{CD}$,故A正确;
当四边形ABCD为平行四边形时,
$\overrightarrow{b}-(\overrightarrow{a}+\overrightarrow{c})$=$\overrightarrow{BC}+\overrightarrow{BA}+\overrightarrow{DA}$=$\overrightarrow{AB}=-\overrightarrow{CD}$,故B不成立;
$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$=$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{DA}$=$\overrightarrow{DC}$,故C错误;
当四边形ABCD为平行四边形时,
$\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$=$\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{AD}$=$\overrightarrow{AB}=-\overrightarrow{CD}$,故D不成立.
故选:A.
点评 本题考查向量的求法,是基础题,解题时要认真审题,注意数形结合思想和向量加法法则的合理运用.

| A. | [2$\sqrt{3}$,+∞) | B. | (-∞,2$\sqrt{3}$] | C. | (-∞,2$\sqrt{3}$]∪(2$\sqrt{3}$,+∞) | D. | [-2$\sqrt{3}$,2$\sqrt{3}$] |
| A. | 45° | B. | 30° | C. | 60° | D. | 30°或150° |
| A. | 平行于同一条直线的两个平面平行或相交 | |
| B. | 平行于同一个平面的两个平面平行 | |
| C. | 平行于同一条直线的两条直线平行 | |
| D. | 平行于同一个平面的两条直线平行或相交 |
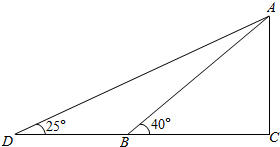 如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)?
如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)?