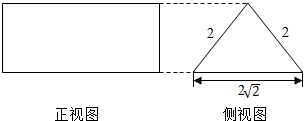
题目内容
3．若f（x）=x3-ax在（-∞，-1）内是增函数，在（-1，1）内是减函数，求a的值．分析 问题转化为-1，1是方程f′（x）=3x2-a=0的2个根，解出即可．
解答 解：若f（x）=x3-ax在（-∞，-1）内是增函数，在（-1，1）内是减函数，
则-1是方程f′（x）=3x2-a=0的根，即x2=$\frac{a}{3}$=1，解得：a=3．
点评 本题考查了导数的应用，考查函数的单调性问题，是一道基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
13．在四边形ABCD中，设$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{BC}=\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{c}$，则$\overrightarrow{CD}$等于（ ）
| A． | $\overrightarrow{c}$-（$\overrightarrow{a}$+$\overrightarrow{b}$） | B． | $\overrightarrow{b}$-（$\overrightarrow{a}+\overrightarrow{c}$） | C． | $\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | D． | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ |
