题目内容
(2008•南京模拟)已知函数y=f (x)的定义域为R,f (27)=3,且对任意的实数x1,x2,必有f (x1•x2)=f (x1)•f (x2) 成立,写出满足条件的一个函数为
y=
| 3 | x |
y=
.| 3 | x |
分析:由题意,函数满足对任意的实数x1,x2,必有f (x1•x2)=f (x1)•f (x2) 成立,考查基本初等函数,幂函数y=f (x)=xn具有这样的性质,故可猜测函数解析式f (x)=xn,再结合题设条件f (27)=3,即可找出符合条件的函数
解答:解:由于(x1•x2)n=(x1)n×(x2)n
∴对于函数y=f (x)=xn,都满足对任意的实数x1,x2,必有f (x1•x2)=f (x1)•f (x2) 成立
又f (27)=3
∴27n=33n=3,解得n=
故满足条件的一个函数是y=
故答案为y=
∴对于函数y=f (x)=xn,都满足对任意的实数x1,x2,必有f (x1•x2)=f (x1)•f (x2) 成立
又f (27)=3
∴27n=33n=3,解得n=
| 1 |
| 3 |
故满足条件的一个函数是y=
| 3 | x |
故答案为y=
| 3 | x |
点评:本题考查根据所给的函数性质求函数解析式,本题是一个开放式题,答案可能不唯一,解题的关键是根据所给的函数性质找出符合条件的函数,即找出具有这种性质的函数函数,这也是本题的难点

练习册系列答案
相关题目
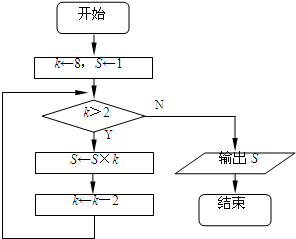 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是