题目内容
已知a,b,c,d均为正实数,且a+b+c+d=1,求证:
+
+
+
≥
.
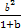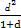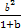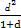+++≥.见解析
证明：因为[(1+a)+(1+b)+(1+c)+(1+d)]·(+++)≥(
·
+
·
+
·
+
·
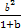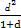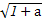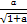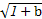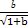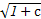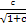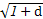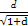)2=(a+b+c+d)2=1,
当且仅当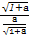
=
=
=
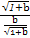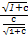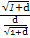即a=b=c=d=
时取等号.
又(1+a)+(1+b)+(1+c)+(1+d)
=4+(a+b+c+d)=5,
所以5(++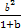+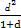)≥1.
所以+++≥.
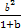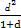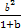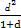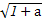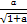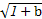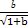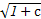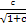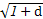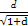+++)≥(·+·+·+·)2=(a+b+c+d)2=1,当且仅当
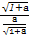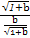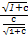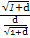===即a=b=c=d=时取等号.又(1+a)+(1+b)+(1+c)+(1+d)
=4+(a+b+c+d)=5,
所以5(
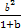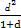+++)≥1.所以
+++≥.
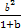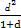练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
≤a2+b2+c2<1.
+
+
的最小值.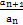
,n∈N+.
·
.
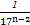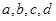满足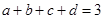
，
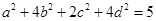，则a的最小值与最大值之差为 .
x＋1＜0.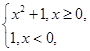
则满足不等式f(1-x2)>f(2x)的x的取值范围是 .
的解集为 ．
的解集为
，则实数
的值为 .