题目内容
(2013•湖州二模)设函数f(x)=
,g(x)=ax2+bx(a,b∈R,a≠0),若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
| 1 |
| x |
分析:画出函数的图象,利用函数的奇偶性,以及二次函数的对称性,即可推出结论.
解答: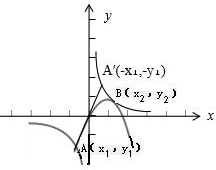 解:当a<0时,作出两个函数的图象,如图,
解:当a<0时,作出两个函数的图象,如图,
因为函数f(x)=
是奇函数,所以A与A′关于原点对称,
显然x2>-x1>0,即x1+x2>0,
-y1>y2,即y1+y2<0;
当a>0时,作出两个函数的图象,同理有x1+x2<0,y1+y2>0.
故选D.
 解:当a<0时,作出两个函数的图象,如图,
解:当a<0时,作出两个函数的图象,如图,因为函数f(x)=
| 1 |
| x |
显然x2>-x1>0,即x1+x2>0,
-y1>y2,即y1+y2<0;
当a>0时,作出两个函数的图象,同理有x1+x2<0,y1+y2>0.
故选D.
点评:本题考查的是函数图象,直接利用图象判断;也可以利用了构造函数的方法,利用函数与导数知识求解.要求具有转化、分析解决问题,由一般到特殊的能力.题目立意较高,很好的考查能力.

练习册系列答案
相关题目
 (2013•湖州二模)已知程序框图如图,则输出的i=
(2013•湖州二模)已知程序框图如图,则输出的i=