题目内容

2．已知抛物线y2=8x的焦点为F，准线为l，则抛物线上满足到定点A（0，4）和准线l的距离相等的点的个数是（　　）
A．0B．1C．2D．3

分析 由抛物线方程求出抛物线的焦点F的坐标，进一步求出AF的中垂线方程，联立直线方程和抛物线方程，由判别式大于0可得答案．

解答 解：如图，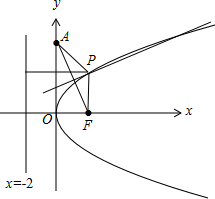

由抛物线y2=8x，得F（2，0），又A（0，4），
∴AF的垂直平分线方程为$y-2=\frac{1}{2}（x-1）$，即x=2y-3．
联立$\left\{\begin{array}{l}{x=2y-3}\\{{y}^{2}=8x}\end{array}\right.$，得y2-16y+24=0，
△=（-16）2-4×24=160＞0，
∴直线y=-2x+4与抛物线y2=8x有两个不同的交点，即抛物线上有两点到A与焦点的距离相等，
也就是抛物线上满足到定点A（0，4）和准线l的距离相等的点的个数是2．
故选：C．

点评 不同考查抛物线的几何性质，考查了抛物线的定义，体现了数学转化思想方法，是中档题．

练习册系列答案
相关题目
12．动点A（x，y）在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转，12秒旋转一周，已知时间t=0时，点A的坐标为（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），则当0≤t≤6时，动点A的纵坐标y的取值范围是（　　）
A．[-$\frac{1}{2}$，1]B．[-1，1]C．[-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$]D．[-$\frac{\sqrt{3}}{2}$，1]
13．椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的两个焦点为F1、F2，点P是椭圆上任意一点（非左右顶点），则△PF1F2的周长为（　　）
A．8B．6C．4D．3
10．已知函数f（x）=x3+ax2+bx图象与直线x-y-4=0相切于（1，f（1））
（1）求实数a，b的值；
（2）若方程f（x）=m-7x有三个解，求实数m的取值范围．
17．已知两个命题p和q，如果p是q的充分不必要条件，那么￢p是￢q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
7．某地近几年粮食需求量逐年上升，如表是部分统计数据：
年份  20062008  20102012  2014
 年需求量（万吨）257  276286  298318 
（1）利用所给数据求年需求量与年份之间的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（2）利用（1）中所求出的直线方程预测该地2015年的粮食需求量．
（参考公式：$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}（{x}_{1}-x）（{y}_{1}-y）}{\underset{\stackrel{n}{∑}}{n+1}（{x}_{1}-x）^{2}}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}（{x}_{1}{y}_{1}）-nxy}{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}^{2}-n{x}^{2}}$，$\widehat{a}$=$\widehat{y}-\widehat{b}x$）
14．直线l经过点P（1，1）且与椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1交于A，B两点，如果点P是线段AB的中点，那么直线l的方程为（　　）
A．3x+2y-5=0B．2x+3y-5=0C．2x-3y+5=0D．3x-2y+5=0
11．已知y=sin（x+$\frac{π}{6}$）图象横坐标缩短为原来的$\frac{1}{2}$（纵坐标不变），再将图象向右平移$\frac{π}{3}$个单位，则对称轴方程为（　　）
A．x=-$\frac{π}{2}$B．x=-$\frac{π}{4}$C．x=$\frac{π}{8}$D．x=$\frac{π}{4}$
12．①已知：3Sn=2an+1，求an
②a1=1，an+1=2an+4，求an．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网