题目内容
已知数列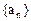 满足
满足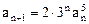 ,
,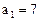 ,求数列
,求数列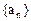 的通项公式。
的通项公式。
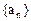 满足
满足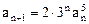 ,
,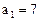 ,求数列
,求数列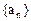 的通项公式。
的通项公式。解:因为 ,所以
,所以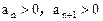 。在
。在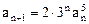 式两边取常用对数得
式两边取常用对数得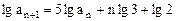 ⑩
⑩
设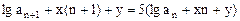 11
11
将⑩式代入11式,得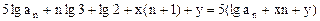 ,两边消去
,两边消去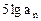 并整理,得
并整理,得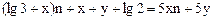 ,则
,则
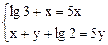 ,故
,故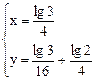
代入11式,得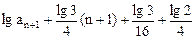
 12
12
由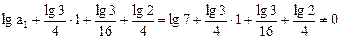 及12式,
及12式,
得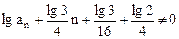 ,
,
则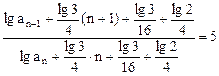 ,
,
所以数列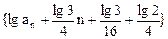 是以
是以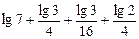 为首项,以5为公比的等比数列,则
为首项,以5为公比的等比数列,则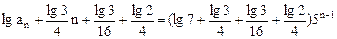 ,因此
,因此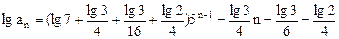
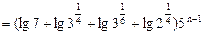
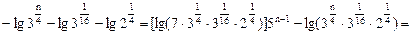
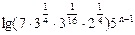
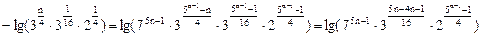 ,则
,则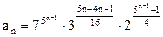 。
。
 ,所以
,所以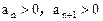 。在
。在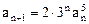 式两边取常用对数得
式两边取常用对数得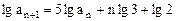 ⑩
⑩设
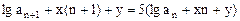 11
11将⑩式代入11式,得
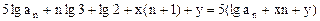 ,两边消去
,两边消去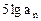 并整理,得
并整理,得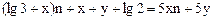 ,则
,则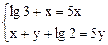 ,故
,故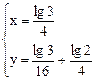
代入11式,得
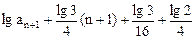
 12
12由
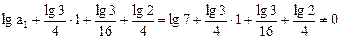 及12式,
及12式,得
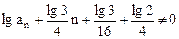 ,
,则
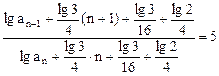 ,
,所以数列
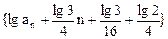 是以
是以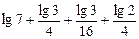 为首项,以5为公比的等比数列,则
为首项,以5为公比的等比数列,则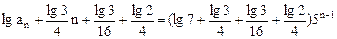 ,因此
,因此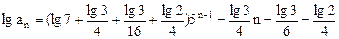
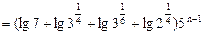
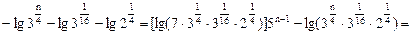
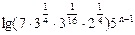
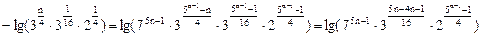 ,则
,则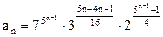 。
。本题解题的关键是通过对数变换把递推关系式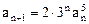 转化为
转化为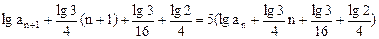 ,从而可知数列
,从而可知数列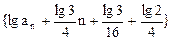 是等比数列,进而求出数列
是等比数列,进而求出数列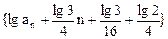 的通项公式,最后再求出数列
的通项公式,最后再求出数列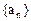 的通项公式。
的通项公式。
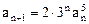 转化为
转化为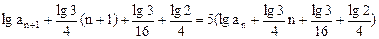 ,从而可知数列
,从而可知数列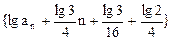 是等比数列,进而求出数列
是等比数列,进而求出数列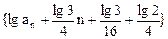 的通项公式,最后再求出数列
的通项公式,最后再求出数列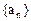 的通项公式。
的通项公式。
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
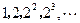 中的第5项到第10项的和为:
中的第5项到第10项的和为: 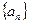 的前
的前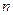 项和为18,前
项和为18,前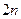 项为和28,则前
项为和28,则前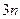 项和为
项和为 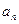 +1=
+1= +
+ (n∈N+),则其{an}的前10项和为
(n∈N+),则其{an}的前10项和为 列
列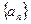 的前
的前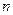 项和为
项和为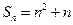 .
.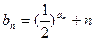 ,求数列
,求数列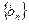 的前
的前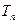 .
.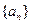 满足
满足 ,其中
,其中 ,函数
,函数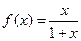 .
. ,
, ,求
,求 ; (2)若数列
; (2)若数列 .数列
.数列 满足
满足 ,求证:
,求证: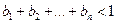 .
.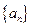 满足:
满足: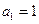 ,且对每个
,且对每个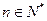 ,
,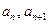 是方程
是方程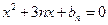 的两根,则
的两根,则 .
.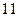
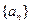 ,
,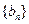 的前
的前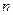 项和分别为
项和分别为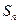 ,
,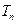 ,若
,若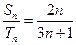 ,则
,则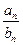 =( )
=( )
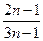
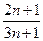
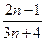
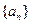 的前
的前 项和为
项和为 ,若
,若 ,
,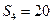 ,则
,则 ( )
( )