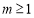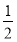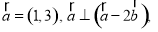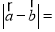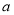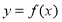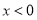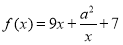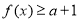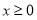题目内容
已知函数 为常数).
为常数).
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)若 ,
, ,求函数
,求函数 的值域;
的值域;
(Ⅲ)若函数 的图像恒在直线
的图像恒在直线 的上方,求实数
的上方,求实数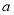 的取值范围.
的取值范围.
(Ⅰ)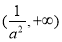 ;(Ⅱ)
;(Ⅱ)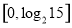 ;(Ⅲ)
;(Ⅲ)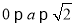 且
且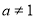
【解析】
试题分析:(1)对数中真数大于0(2)思路:要先求真数的范围再求对数的范围。求真数范围时用配方法,求对数范围时用点调性(3)要使函数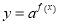 的图像恒在直线
的图像恒在直线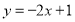 的上方,则有
的上方,则有 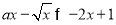 在
在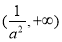 上恒成立。把
上恒成立。把 看成整体,令
看成整体,令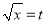 即
即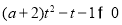 在
在 上恒成立,转化成单调性求最值问题
上恒成立,转化成单调性求最值问题
试题解析:(Ⅰ)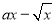
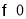
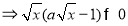
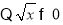
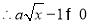
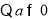

 所以定义域为
所以定义域为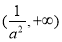
(Ⅱ)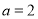 时
时 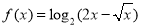 令
令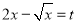 则
则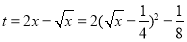
因为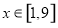 所以
所以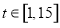 ,所以
,所以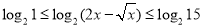 即
即
所以函数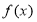 的值域为
的值域为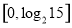
(Ⅲ)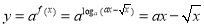
要使函数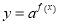 的图像恒在直线
的图像恒在直线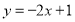 的上方
的上方
则有 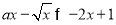 在
在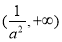 上恒成立。 令
上恒成立。 令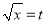 则
则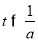
即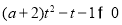 在
在 上恒成立
上恒成立
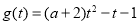 的图像的对称轴为
的图像的对称轴为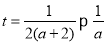 且
且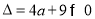
所以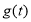 在
在 上单调递增,要想
上单调递增,要想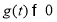 恒成立,只需
恒成立,只需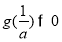
即

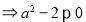
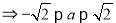
因为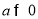 且
且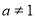 所以
所以 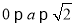 且
且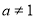
考点:(1)对数的定义域(2)对数的单调性(3)恒成立问题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目