Question

17．已知扇形圆心角的弧度数为2，圆心角所对的弦长为4，则这个扇形的面积是$\frac{4}{{{{sin}^2}1}}$．

Answer 1

分析 由题意表示出扇形的半径和弧长，代入弧长公式计算可得．

解答 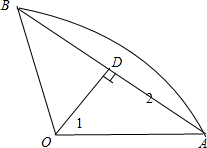解：由题意可得RT△AOD中∠AOD=1，AD=2，
由$\frac{AD}{OA}$=sin1可得扇形的半径r=OA=$\frac{2}{sin1}$，
∴扇形的弧长l=αr=$\frac{4}{sin1}$，
∴扇形的面积S=$\frac{1}{2}$lr=$\frac{4}{{{{sin}^2}1}}$
故答案为：$\frac{4}{{{{sin}^2}1}}$

点评 本题考查扇形的面积公式，属基础题．