题目内容
已知f(x)＝(x－1)2，数列{an}是首项为a1，公差为d的等差数列；{bn}是首项为b1，公比为q(q∈R且q≠1)的等比数列，且满足a1＝f(d－1)，a3＝f(d＋1)，b1＝f(q＋1)，b3＝f(q－1)．
(Ⅰ)求数列{an}和{bn}的通项公式；
(Ⅱ)若存在cn＝an·bn(n∈N*)，试求数列{cn}的前n项和；
(Ⅲ)是否存在数列{dn}，使得
对一切大于1的正整数n都成立，若存在，求出{dn}；若不存在，请说明理由．
答案：
解析：
解析：
|
(Ⅰ) (Ⅱ)由错位相减法，可得 (Ⅲ)假设存在满足条件的数列 解法1： 两边同除以 令 解法2：由迭代法可得 |
；
．
，则有
，且有
，
可得
，
，则有
，故
是首项为－1，公差为
的等差数列，则
，故
．
练习册系列答案
小学教材完全解读系列答案
相关题目
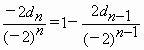满足：当|x|≤1时，有
恒成立，求函数f(x)的解析表达式；
，证明：
与
不可能垂直．
(x∈R)，在区间[－1，1]上是增函数．
的两个非零实根为x1、x2，试问：是否存在实数m，使得不等式m2＋tm＋1≥|x1－x2|对任意a∈A及t∈[－1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由．
