Question

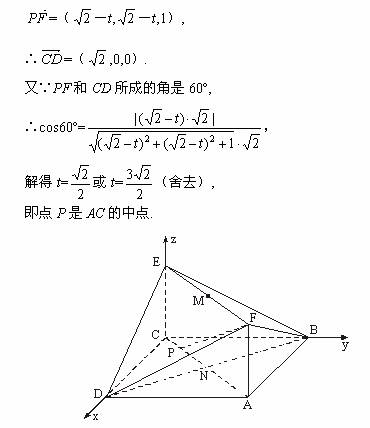
19.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=，AF=1,M是线段EF的中点.

（Ⅰ）求证:AM∥平面BDE;

（Ⅱ）求二面角A－DF－B的大小;

（Ⅲ）试在线段AC上确定一点P,使得PF与BC所成的角是60°.

Answer 1

19.本题主要考查空间线面关系及空间向量概念与运算等基础知识,同时考查空间想象能力和推理运算能力.

方法一：

解：（Ⅰ）记AC与BD的交点为O,连结OE,

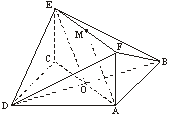
∵O、M分别是AC、EF的中点,ACEF是矩形,

∴四边形AOEM是平行四边形.

∴AM∥OE.

∵OE平面BDE,AM平面BDE,

∴AM∥平面BDE.

（Ⅱ）在平面AFD中过A作AS⊥DF于S,连结BS,

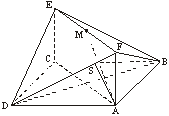
∵AB⊥AF,AB⊥AD,AD∩AF=A,

∴AB⊥平面ADF，

∴AS是BS在平面ADF上的射影,

由三垂线定理得BS⊥DF.

∴∠BSA是二面角A－DF－B的平面角.

在Rt△ASB中，AS=，AB=，

∴tanASB=,∠ASB=60°.

∴二面角A－DF－B的大小为60°.

（Ⅲ）设CP=t（0≤t≤2）,作PQ⊥AB于Q,则PQ∥AD,

 

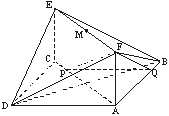
∵PQ⊥AB,PQ⊥AF,AB∩AF=A,

∴PQ⊥平面ABF,QF平面ABF，

∴PQ⊥QF.

在Rt△PQF中,∠FPQ=60°,

PF=2PQ.

∵△PAQ为等腰直角三角形,

∴PQ=（2－t）.

又∵△PAF为直角三角形,

∴PF=，

∴=2·（2－t）.

所以t=1或t=3（舍去）.

即点P是AC的中点.

方法二：

（Ⅰ）建立如图所示的空间直角坐标系.

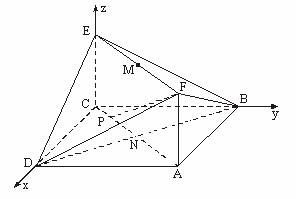
设AC∩BD=N,连结NE,

则点N、E的坐标分别是（,,0）、（0,0,1）,

∴=（－,－,1）.

又点A、M的坐标分别是

（,,0）、（,,1）,

∴=（－,－,1）.

∴=且NE与AM不共线，

∴NE∥AM.

又∵NE平面BDE,AM平面BDE,

∴AM∥平面BDE.

（Ⅱ）∵AF⊥AB,AB⊥AD,AF∩AD=A,

∴AB⊥平面ADF.

∴=（－,0,0）为平面DAF的法向量.

∵·=（－,－,1）·（－,,0）=0,

·=（－,－,1）·（,,1）=0得

⊥,⊥,

∴为平面BDF的法向量.

∴cos〈,〉=.

∴与的夹角是60°.

即所求二面角A－DF－B的大小是60°.

（Ⅲ）设P（t,t,0）（0≤t≤）得