题目内容
 如图,已知圆O:x2+y2=1,O为坐标原点.
如图,已知圆O:x2+y2=1,O为坐标原点.(1)边长为
| 2 |
①求轨迹E的方程;
②过轨迹E上一定点P(x0,y0)作相互垂直的两条直线l1,l2,并且使它们分别与圆O、轨迹E相交,设l1被圆O截得的弦长为a,设l2被轨迹E截得的弦长为b,求a+b的最大值.
(2)正方形ABCD的一边AB为圆O的一条弦,求线段OC长度的最值.
分析:(1)①由题意知OA2+OB2=AB2,∠OBA=
,∠OBC=
,在△OBC中,OC2=OB2+BC2-2OB•BC=5.由此可知轨迹E的方程;②设点O到直线l1,l2的距离分别为d1,d2,因为l1⊥l2,所以d12+d22=OP2=x02+y02=5,由此可知(a+b)2=4[6-(d12≤4[6-(d12+d22)+2•
]=4[12-2(d12+d22)]=4(12-10)=8,即a+b的最大值.
(2)设正方形边长为a,∠OBA=θ,则cosθ=
,θ∈[0,
).当A、B、C、D按顺时针方向时,如图所示,在△OBC中,a2+1-2acos(
+θ)=OC2,由2θ+
∈[
,
),此时OC∈(1,
+1];当A、B、C、D按逆时针方向时,在△OBC中,a2+1-2acos(
-θ)=OC2,OC∈[
-1,
).由此可知,线段OC长度的最小值为
-1,最大值为
+1.
| π |
| 4 |
| 3π |
| 4 |
| 6-d12-d22 |
| 2 |
(2)设正方形边长为a,∠OBA=θ,则cosθ=
| a |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| 2 |
| π |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
解答: 解:(1)①如图连接OB,OA,因为OA=OB=1,AB=
解:(1)①如图连接OB,OA,因为OA=OB=1,AB=
,所以OA2+OB2=AB2,
所以∠OBA=
,所以∠OBC=
,在△OBC中,OC2=OB2+BC2-2OB•BC=5,(2分)
所以轨迹E是以O为圆心,
为半径的圆,
所以轨迹E的方程为x2+y2=5;(3分)
②设点O到直线l1,l2的距离分别为d1,d2,
因为l1⊥l2,所以d12+d22=OP2=x02+y02=5,(5分)
则a+b=2
+2
,
则(a+b)2=4[6-(d12
≤4[6-(d12+d22)+2•
]=4[12-2(d12+d22)]=4(12-10)=8,(8分)
当且仅当
,即
时取“=”,
所以a+b的最大值为2
;(9分)
(2)设正方形边长为a,∠OBA=θ,则cosθ=
,θ∈[0,
).
当A、B、C、D按顺时针方向时,如图所示,在△OBC中,a2+1-2acos(
+θ)=OC2,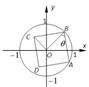
即OC=
=
=
=
,
由2θ+
∈[
,
),此时OC∈(1,
+1];(12分)
当A、B、C、D按逆时针方向时,在△OBC中,a2+1-2acos(
-θ)=OC2,
即OC=
=
=
=
,
由2θ-
∈[-
,
),此时OC∈[
-1,
),(15分)
综上所述,线段OC长度的最小值为
-1,最大值为
+1.(16分)
 解:(1)①如图连接OB,OA,因为OA=OB=1,AB=
解:(1)①如图连接OB,OA,因为OA=OB=1,AB=| 2 |
所以∠OBA=
| π |
| 4 |
| 3π |
| 4 |
所以轨迹E是以O为圆心,
| 5 |
所以轨迹E的方程为x2+y2=5;(3分)
②设点O到直线l1,l2的距离分别为d1,d2,
因为l1⊥l2,所以d12+d22=OP2=x02+y02=5,(5分)
则a+b=2
| 1-d12 |
| 5-d22 |
则(a+b)2=4[6-(d12
≤4[6-(d12+d22)+2•
| 6-d12-d22 |
| 2 |
当且仅当
|
|
所以a+b的最大值为2
| 2 |
(2)设正方形边长为a,∠OBA=θ,则cosθ=
| a |
| 2 |
| π |
| 2 |
当A、B、C、D按顺时针方向时,如图所示,在△OBC中,a2+1-2acos(
| π |
| 2 |

即OC=
| (2cosθ)2+1+2•2cosθ•sinθ |
| 4cos2θ+1+2sin2θ |
| 2cos2θ+2sin2θ+3 |
2
|
由2θ+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| 2 |
当A、B、C、D按逆时针方向时,在△OBC中,a2+1-2acos(
| π |
| 2 |
即OC=
| (2cosθ)2+1-2•2cosθ•sinθ |
| 4cos2θ+1-2sin2θ |
| 2cos2θ-2sin2θ+3 |
-2
|
由2θ-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 2 |
| 5 |
综上所述,线段OC长度的最小值为
| 2 |
| 2 |
点评:本题考查直线和圆锥曲线的位置关系,解题时要注意数形结合.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为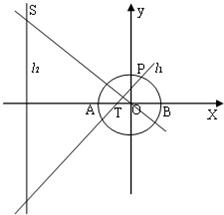 如图,已知圆O:x2+y2=2交x轴于A、B两点,P在圆O上运动(不与A、B重合),过P作直线l1,OS垂直于l1交直线l2:x=-3于点S.
如图,已知圆O:x2+y2=2交x轴于A、B两点,P在圆O上运动(不与A、B重合),过P作直线l1,OS垂直于l1交直线l2:x=-3于点S.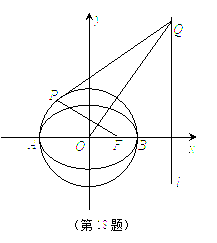 如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为