题目内容
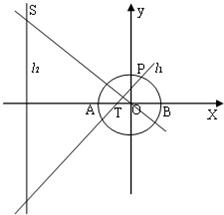 如图,已知圆O:x2+y2=2交x轴于A、B两点,P在圆O上运动(不与A、B重合),过P作直线l1,OS垂直于l1交直线l2:x=-3于点S.
如图,已知圆O:x2+y2=2交x轴于A、B两点,P在圆O上运动(不与A、B重合),过P作直线l1,OS垂直于l1交直线l2:x=-3于点S.(1)求证:“如果直线l1过点T(-1,0),那么
| OP |
| PS |
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
分析:(1)设P(x0,y0),则x02+y02=2,当x0=-1时,求出S的坐标,化简
•
的解析式.当x0≠-1时,求出S的坐标,
化简
•
的解析式.
(2)先写出逆命题,设S(-3,t),P(x0,y0)(y0≠0),由
•
=1,及x02+y02=2,得出t=
.
当当x0=-1时,直线l1的方程知过点(-1,0);当x0≠-1时,由直线l1的方程知过点(-1,0).
| OP |
| PS |
化简
| OP |
| PS |
(2)先写出逆命题,设S(-3,t),P(x0,y0)(y0≠0),由
| OP |
| PS |
| 3+3x0 |
| y0 |
当当x0=-1时,直线l1的方程知过点(-1,0);当x0≠-1时,由直线l1的方程知过点(-1,0).
解答:证明:(1)设P(x0,y0)(y0≠0),则x02+y02=2.当x0=-1时,
∵直线l1过点T(-1,0),∴S(-3,0),即
=(-3-x0,-y0),
∴
•
=-3x0-x02-y02=1.
当x0≠-1时,∵直线l1过点T(-1,0),∴直线l1的斜率k1=
,
∴直线OS的斜率k=-
,其方程为 y=-
x,
∴S(-3,
),即
=(-3-x0,
-y0).
∴
•
=-3x0-x02+3x0+3-y02=3-2=1.
故“如果直线l1过点T(-1,0),那么
•
=1”为真命题.
(2)逆命题为:如果
•
=1,那么直线l1过点T(-1,0).逆命题也为真命题,以下给出证明:
设S(-3,t),P(x0,y0)(y0≠0),则
=(-3-x0,t-y0),
∵
•
=1,∴-3x0-x02+ty0-y02=1,又x02+y02=2,
∴t=
.当x0=-1时,直线l1的方程为x=-1,显然过点(-1,0);
当x0≠-1时,直线OS的斜率k=
,∴直线l1的方程为y-y0=
(x-x0),令y=0,得x=-1,
∴直线l1过定点(-1,0).综上,直线l1恒过定点(-1,0).
∵直线l1过点T(-1,0),∴S(-3,0),即
| PS |
∴
| OP |
| PS |
当x0≠-1时,∵直线l1过点T(-1,0),∴直线l1的斜率k1=
| y0 |
| x0+1 |
∴直线OS的斜率k=-
| x0+1 |
| y0 |
| x0+1 |
| y0 |
∴S(-3,
| 3x0+3 |
| y0 |
| PS |
| 3x0+3 |
| y0 |
∴
| OP |
| PS |
故“如果直线l1过点T(-1,0),那么
| OP |
| PS |
(2)逆命题为:如果
| OP |
| PS |
设S(-3,t),P(x0,y0)(y0≠0),则
| PS |
∵
| OP |
| PS |
∴t=
| 3+3x0 |
| y0 |
当x0≠-1时,直线OS的斜率k=
| x0+1 |
| -y0 |
| y0 |
| x0+1 |
∴直线l1过定点(-1,0).综上,直线l1恒过定点(-1,0).
点评:本题考查直线和圆相交的性质,四种命题的真假关系,两个向量的数量积的运算以及求两直线交点的坐标.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图,已知圆O:x2+y2=1,O为坐标原点.
如图,已知圆O:x2+y2=1,O为坐标原点. 如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为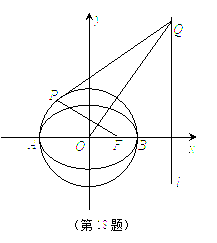 如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为