Question

【题目】在平面直角坐标系中，MBC顶点的坐标为A(-1，2)，B(1，4)，C(3，2).

(1)求ΔABC外接圆E的方程；

(2)若直线经过点(0，4)，且与圆E相交所得的弦长为，求直线的方程；

(3)在圆E上是否存在点P，满足，若存在，求出点P的坐标；若不存在，请说明理由.

Answer 1

【答案】(1) ；(2) 或； (3)不存在，理由见解析.

【解析】

（1）利用待定系数法求△ABC外接圆E的方程；
（2）分类讨论，利用韦达定理，结合弦长公式，求直线的方程；
（3）求出P的轨迹方程，与圆E联立，即可得出结论．

解：(1)设圆的一般方程为，

则，解得，

∴ΔABC外接圆E的方程为；

(2)①当直线的斜率不存在时，直线的方程为，

联立，解得或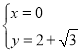

此时弦长为，满足题意，

②当直线的斜率存在时，设直线的方程为，即

联立，得，

，解得或，

设直线与圆交于点E(，)，点F(，)，

则，

∵弦长为，

∴，

解得，

∴直线的方程为，

综上所求：直线的方程为或；

(3)假设存在点，设出点P的坐标为(，)，

∵，A(-1，2)，B(1，4)，

∴，即，

联立，两式相减得，

联立，方程组无解，

∴圆E上不存在点P，满足.