题目内容
求函数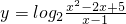 的值域.
的值域.
解:由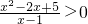 可知x>1,
可知x>1,
设g(x)=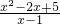 ,
,
则g(x)=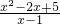 =x-1
=x-1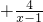 ≥2
≥2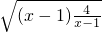 =4,
=4,
即真数的最小值为4,又以2为底的对数函数为增函数,
所以y≥log24=2,即原函数的值域为[2,+∞).
分析:即找y=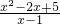 在
在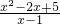 >0时的值域用分离常数法.
>0时的值域用分离常数法.
点评:若函数为分式结构,且分子分母中有未知数的平方,求值域时常考虑分离常数法,或用判别式法
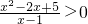 可知x>1,
可知x>1,设g(x)=
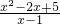 ,
,则g(x)=
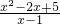 =x-1
=x-1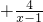 ≥2
≥2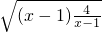 =4,
=4,即真数的最小值为4,又以2为底的对数函数为增函数,
所以y≥log24=2,即原函数的值域为[2,+∞).
分析:即找y=
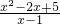 在
在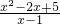 >0时的值域用分离常数法.
>0时的值域用分离常数法.点评:若函数为分式结构,且分子分母中有未知数的平方,求值域时常考虑分离常数法,或用判别式法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
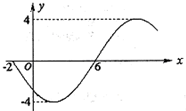 函数
函数