题目内容
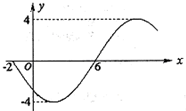函数y=Asin(ωx+?)(ω＞0，|?|＜| π | 2 |
（1）求函数的最小正周期；（2）求函数解析式；（3）当x∈（-2，8）时，求函数的值域．
分析：（1）由周期公式
T=
=6-（-2）=8可求其最小正周期；
（2）由周期T=
=16可求得由ω，由函数的最值结合图象特征可求得A，进一步可求得φ，从而可求得函数解析式；
（3）由（2）求得y=-4sin（
x+
），由x∈（-2，8），可求得
x+
∈（0，
），由y=-4sinx，x∈（0，
）即可求得函数的值域．
| 1 |
| 2 |
| π |
| ω |
（2）由周期T=
| 2π |
| ω |
（3）由（2）求得y=-4sin（
| π |
| 8 |
| π |
| 4 |
| π |
| 8 |
| π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
解答：解：（1）∵
T=
=6-（-2）=8，∴T=16，
（2）∵T=
=16，∴ω=
，
由图象及其特征可知A=-4，及-2×
+φ=0，解得φ=
，
∴y=-4sin（
x+
）；
（3）∵x∈（-2，8），
∴
x+
∈（0，
），
∴y=-sin（
x+
）∈[-1，
），
∴y=-4sin（
x+
）∈[-4，2
），
∴当x∈（-2，8）时，函数的值域为[-4，2
）．
| 1 |
| 2 |
| π |
| ω |
（2）∵T=
| 2π |
| ω |
| π |
| 8 |
由图象及其特征可知A=-4，及-2×
| π |
| 8 |
| π |
| 4 |
∴y=-4sin（
| π |
| 8 |
| π |
| 4 |
（3）∵x∈（-2，8），
∴
| π |
| 8 |
| π |
| 4 |
| 5π |
| 4 |
∴y=-sin（
| π |
| 8 |
| π |
| 4 |
| ||
| 2 |
∴y=-4sin（
| π |
| 8 |
| π |
| 4 |
| 2 |
∴当x∈（-2，8）时，函数的值域为[-4，2
| 2 |
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，难点在于求A时需根据函数的最值及图象特征求得A=-4，φ=
；易错点在于当x∈（-2，8），求函数的值域时，易忽略符号的正负的判断，属于中档题．
| π |
| 4 |
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
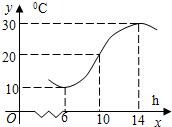如图所示，某地一天从6时到14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b，则8时的温度大约为
如图，是函数y=Asin（ωx+φ），（-π＜φ＜π）的图象的一段，O是坐标原点，P是图象的最高点，A点坐标为（5，0），若