题目内容
1.等差数列{an}中,S5=28,S10=36,则S15等于24.分析 由等差数列的性质得S5,S10-S5,S15-S10成等差数列,由此能求出结果.
解答 解:∵等差数列{an}中,S5=28,S10=36,
由等差数列的性质得S5,S10-S5,S15-S10也成等差数列,
∴28,8,S15-36成等差数列,
∴2×8=28+S15-36,
则S15=24.
故答案为:24.
点评 本题考查等差数列的前15项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
11.设向量$\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(cosα,-$\frac{1}{3}$)(0°<α<180°),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则角α为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
12.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y+(a2-1)=0平行而不重合,则a等于( )
| A. | -1或2 | B. | -1 | C. | 2 | D. | $\frac{2}{3}$ |
6.若三点A(0,a,2b),B(2,3,4),C(3,4,5)共线,则下列等式成立的是( )
| A. | 2a=b | B. | a+b=2 | C. | 2a-b=3 | D. | a-2b=1 |
10.已知sin(π-α)=-$\frac{2}{5}$,且α是第四象限角,则tanα=( )
| A. | $\frac{2\sqrt{21}}{21}$ | B. | -$\frac{2\sqrt{21}}{21}$ | C. | -$\frac{2}{3}$ | D. | $\frac{\sqrt{21}}{2}$ |
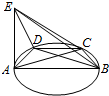 已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).
已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).