题目内容
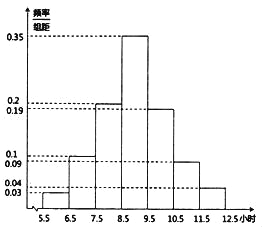
【题目】某中学有初中学生1800人,高中学生1200人. 为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并分别加以统计,得到如图所示的频率分布直方图.
,并分别加以统计,得到如图所示的频率分布直方图.
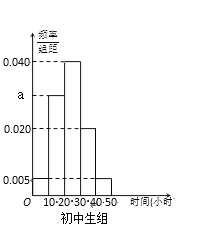
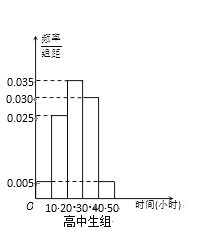
(Ⅰ)写出![]() 的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(Ⅱ)从阅读时间不足10个小时的样本学生中随机抽取2人,求至少抽到1名高中生的概率.
【答案】(Ⅰ)![]() ;870人 (Ⅱ)
;870人 (Ⅱ)![]()
【解析】
(Ⅰ)根据频率频率直方图的性质可求得![]() 的值;由分层抽样求得初中生有60名,高中有
的值;由分层抽样求得初中生有60名,高中有
40名,再求阅读时间不小于30小时的学生的频率及人数再求和即得解;
(Ⅱ)利用古典概型的概率公式求至少抽到1名高中生的概率.
(Ⅰ)解:由频率直方图的性质,![]() ,所以
,所以![]() ,
,
由分层抽样,知抽取的初中生有60名,高中生有40名.
因为初中生中,阅读时间不小于30个小时的学生频率为![]() ,
,
所以所有的初中生中,阅读时间不小于30个小时的学生约有![]() 人,
人,
同理,高中生中,阅读时间不小于30个小时的学生频率为![]() ,学生人数约有
,学生人数约有![]() 人.
人.
所以该校所有学生中,阅读时间不小于30个小时的学生人数约有![]() 人.
人.
(Ⅱ)解:记“从阅读时间不足10个小时的样本学生中随机抽取2人,至少抽到1名高中生”为事件![]() ,
,
初中生中,阅读时间不足10个小时的学生频率为![]() ,样本人数为
,样本人数为![]() 人.
人.
高中生中,阅读时间不足10个小时的学生频率为![]() ,样本人数为
,样本人数为![]() 人.
人.
记这3名初中生为![]() ,这2名高中生为
,这2名高中生为![]() ,
,
则从阅读时间不足10个小时的样本学生中随机抽取2人,所有可能结果有10种,即:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而事件![]() 的结果有7种,它们是
的结果有7种,它们是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.

【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.