题目内容
【题目】设F是椭圆C：
（a＞b＞0）的一个焦点，P是椭圆C上的点，圆x2＋y2＝
与线段PF交于A，B两点，若A，B三等分线段PF，则椭圆C的离心率为（ ）
A.
B.
C.
D.
【答案】D
【解析】
取线段PF的中点H，连接OH，OA，由题意可得OH⊥AB，设|OH|＝d，根据椭圆的定义以及在Rt△OHA中，可得a＝5d，在Rt△OHF中，利用勾股定理即可求解.
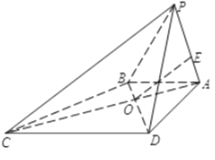
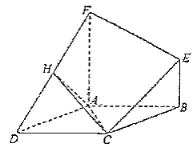
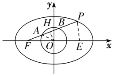
如图，取线段PF的中点H，连接OH，OA.
设椭圆另一个焦点为E，连接PE.
∵A，B三等分线段PF，∴H也是线段AB的中点，即OH⊥AB.
设|OH|＝d，则|PE|＝2d，|PF|＝2a－2d，|AH|＝
.
在Rt△OHA中，|OA|2＝|OH|2＋|AH|2，解得a＝5d.
在Rt△OHF中，|FH|＝
，|OH|＝
，|OF|＝c.
由|OF|2＝|OH|2＋|FH|2，
化简得17a2＝25c2，
.
即椭圆C的离心率为
.
故选：D.
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
【题目】甲、乙两台机床生产同一型号零件，记生产的零件的尺寸为
，相关行业质检部门规定：若
，则该零件为优等品；若
，则该零件为中等品；其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件，经质里检测得到下表数据：
尺寸 |
|
|
|
|
|
|
甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
（Ⅰ）设生产每件产品的利润为：优等品3元，中等品1元，次品亏本1元.若将频率视为概率，试估算甲机床生产一件零件的利润的数学期望；
（Ⅱ）根据已知条件完成下面的列联表，并据此数据回答：是否有
的把握认为“零件优等与否和所用机床有关”？
甲机床 | 乙机床 | 合计 | |
优等品 | |||
非优等品 | |||
合计 |