题目内容
已知 是
是 上的奇函数,对
上的奇函数,对 都有
都有 成立,若
成立,若 ,则
,则 等于
等于
A. | B. | C. | D. |
C.
解析试题分析:令x=-2,则f(-2+4)=f(-2)+f(2),又因为f(x)在R上是奇函数.,所以f(-2)+f(2)=0,即f(2)=0.所以得到f(x+4)=f(x).所以函数是以4为周期的周期函数.所以f(2014)=f(2)=0.本题的关键是把奇函数与所给的式子结合起来得到周期为四的结果.注 这个条件多余.
这个条件多余.
考点:1.奇函数.2.周期函数.3.递推的思想.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
若 为偶函数,且
为偶函数,且 是
是 的一个零点,则-
的一个零点,则- 一定是下列哪个函数的零点( )
一定是下列哪个函数的零点( )
A. | B. |
C. | D. |
下列函数中,在其定义域中,既是奇函数又是减函数的是( )
A. | B. | C. | D. |
函数 的零点个数为( )
的零点个数为( )
A. | B.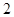 | C. | D. |
函数 的值域是( )
的值域是( )
| A.[-1,1] | B.(-1,1) | C.[-1,1) | D.(-1,1] |
函数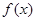 的定义域为
的定义域为 ,且满足:
,且满足: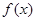 是偶函数,
是偶函数,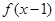 是奇函数,若
是奇函数,若 ,则
,则 ( )
( )
A. 9 9 | B.9 | C. 3 3 | D.0 |
已知 若
若 则
则 等于 ( )
等于 ( )
A. | B. | C.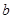 | D. |

 为
为 的导函数,则
的导函数,则
 满足条件:(1)
满足条件:(1) 、
、 的图象上,(2)
的图象上,(2) 的图象与函数
的图象与函数 的图象中“和谐点对”的个数是( )
的图象中“和谐点对”的个数是( )