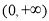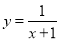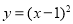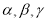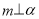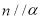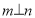题目内容
若非零函数 对任意实数
对任意实数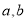 均有
均有 ,且当
,且当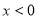 时,
时, .
.
(1)求证:
(2)求证: 为减函数;
为减函数;
(3)当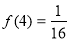 时,解不等式
时,解不等式
(1)见解析(2)见解析(3)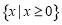
【解析】
试题分析:(1)赋值法,令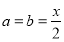 ,有
,有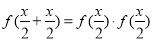 ; (2)令
; (2)令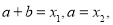 则
则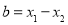 ;将上述三式代入:
;将上述三式代入: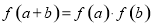 得:
得: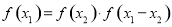
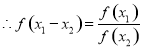 ,接下来就可用定义法证明
,接下来就可用定义法证明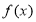 为减函数.
为减函数.
(3)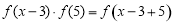 ,由
,由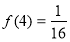 可得
可得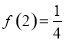 ,再利用(2)的结论转化为解一次不等式.
,再利用(2)的结论转化为解一次不等式.
试题解析:
【解析】
(1)令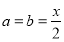 ,有
,有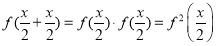 ;
;
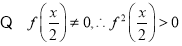
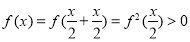 4分[
4分[
(2)令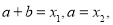 则
则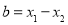 ;
;
将上述三式代入: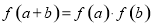
得: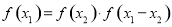
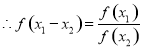
设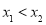 则
则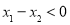
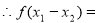
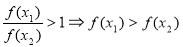 ,
,

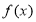 为减函数 8分
为减函数 8分
(3)由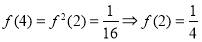
原不等式转化为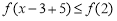 ,结合(2)
,结合(2)
得: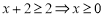
故不等式的解集为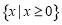 13分
13分
考点:1、赋值法解决抽象函数问题;2、函数单调性的证明及应用.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目