题目内容
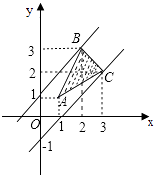
【题目】在直角坐标系xOy中，已知点A（1，1），B（2，3），C（3，2），点P（x，y）在△ABC三边围成的区域（含边界）上．
（1）若 
，求| 
|；
（2）设 =m 
+n 
（m，n∈R），用x，y表示m﹣n，并求m﹣n的最大值．
【答案】
（1）解：∵A（1，1），B（2，3），C（3，2）， 
，
∴（1﹣x，1﹣y）+（2﹣x，3﹣y）+（3﹣x，2﹣y）=0
∴3x﹣6=0，3y﹣6=0
∴x=2，y=2，
即 
=（2，2）
∴ 
（2）解：∵A（1，1），B（2，3），C（3，2），
∴ 
， 
∵ =m 
+n 
，
∴（x，y）=（m+2n，2m+n）
∴x=m+2n，y=2m+n
∴m﹣n=y﹣x，
令y﹣x=t，由图知，当直线y=x+t过点B（2，3）时，t取得最大值1，
故m﹣n的最大值为1．
【解析】（1）先根据 ，以及各点的坐标，求出点p的坐标，再根据向量模的公式，问题得以解决；（2）利用向量的坐标运算，先求出 ， ，再根据 =m +n ，表示出m﹣n=y﹣x，最后结合图形，求出m﹣n的最小值．
【考点精析】掌握平面向量的基本定理及其意义和平面向量的坐标运算是解答本题的根本，需要知道如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
；坐标运算：设
，
则
;
;设
，则
．
练习册系列答案
相关题目
